Radicali¶
Radici¶
Radici quadrate¶
Ricordiamo che il quadrato di un numero reale r è il numero che si ottiene
moltiplicando r per se stesso. Il quadrato di un numero è sempre un numero non
negativo; numeri opposti hanno lo stesso quadrato:
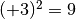 ;
;
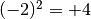 ;
;
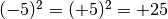 .
.
L’operazione inversa dell’elevamento al quadrato si chiama radice quadrata. La
radice quadrata di un numero reale
 è allora quel numero che elevato al quadrato, cioè, che moltiplicato per se
stesso, dà il numero
è allora quel numero che elevato al quadrato, cioè, che moltiplicato per se
stesso, dà il numero
 .
.
Osserviamo che non esiste la radice quadrata di un numero negativo, poiché non esiste nessun numero che elevato al quadrato possa dare come risultato un numero negativo.
DEFINIZIONE. Si dice radice quadrata di un numero reale positivo o nullo quel numero reale positivo o nullo che elevato al quadrato dà come risultato il numero dato.
In simboli
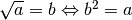 dove
dove
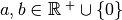 .
.
Il simbolo
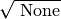 è il simbolo della radice quadrata; il numero a è detto radicando, il numero b
è detto radice quadrata di
è il simbolo della radice quadrata; il numero a è detto radicando, il numero b
è detto radice quadrata di
 .
.
Dalla definizione
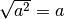 con
con
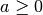 .
.
Per esempio
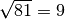 perché
perché
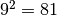 ;
;
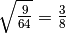 perché
perché
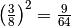 .
.
Osserva ora che
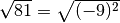 ma non è vero che
ma non è vero che
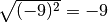 perché nella definizione di radice quadrata abbiamo imposto che il risultato
dell’operazione di radice quadrata sia sempre un numero positivo o nullo.
perché nella definizione di radice quadrata abbiamo imposto che il risultato
dell’operazione di radice quadrata sia sempre un numero positivo o nullo.
Per confrontare due numeri reali, osserviamo prima di tutto i segni. Se i segni dei numeri sono discordi, il numero n
Questa osservazione ci induce a porre molta attenzione quando il radicando è
un’espressione letterale: in questo caso
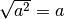 non è del tutto corretto poiché a può assumere sia valori positivi sia valori
negativi. Scriveremo correttamente
non è del tutto corretto poiché a può assumere sia valori positivi sia valori
negativi. Scriveremo correttamente
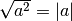 .
.
Esempi
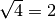 infatti
infatti
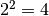
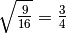 infatti
infatti
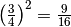
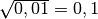 infatti
infatti
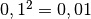
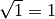 infatti
infatti
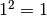
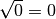 infatti
infatti
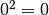
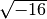 non esiste, radicando negativo.
non esiste, radicando negativo.
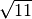 esiste ma non è un numero intero né razionale, è un numero irrazionale.
esiste ma non è un numero intero né razionale, è un numero irrazionale.
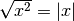 dobbiamo mettere il valore assoluto al risultato perché non conoscendo il
segno di x dobbiamo imporre che il risultato sia sicuramente positivo.
dobbiamo mettere il valore assoluto al risultato perché non conoscendo il
segno di x dobbiamo imporre che il risultato sia sicuramente positivo.
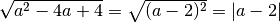 dobbiamo mettere il valore assoluto perché a-2 può anche essere negativo.
dobbiamo mettere il valore assoluto perché a-2 può anche essere negativo.
Radici cubiche¶
Definizione: Si dice radice cubica di un numero reale
 quel numero che, elevato al cubo, dà come risultato
quel numero che, elevato al cubo, dà come risultato
 . In simboli
. In simboli
![\sqrt[3 ]{a } = b \Leftrightarrow b ^{3 } = a](_images/math/4d64e56902a373647892cb4072f565bc5c1a482b.png) dove
dove
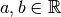 .
.
Puoi notare che la radice cubica di un numero reale esiste sempre sia per i numeri positivi o nulli, sia per i numeri negativi.
Esempi
![\sqrt[3 ]{- 8 } = - 2](_images/math/e194fc4610c08af5a3fd4736308632eea447b06b.png) infatti
infatti
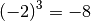
![\sqrt[3 ]{125 } = 5](_images/math/07bea0f07e81491dec7bd40ef84abc7f7ab06d35.png) infatti
infatti
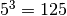
![\sqrt[3 ]{1 } = 1](_images/math/048913b794a8c0becd2c79c8915bea2a54a492b8.png) infatti
infatti
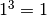
![\sqrt[3 ]{0 } = 0](_images/math/6f1c9c92eb0da0f76c4785157c87ac23784bbd79.png) infatti
infatti
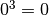
![\sqrt[3 ]{- 1000 } = - 10](_images/math/ef2852269841c5d2b749ffacb4302c9f3e98ace7.png) infatti
infatti
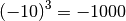
![\sqrt[3 ]{\frac{1 }{8 } } = \frac{1 }{2 }](_images/math/fccafe86778ecd60b7eabf97460d53a640e61c14.png) infatti
infatti
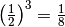
![\sqrt[3 ]{0,125 } = 0,5](_images/math/bfa85962cb66fc94953b7ee1604d6a26a4a65dfe.png) infatti
infatti
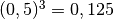
![\sqrt[3 ]{x ^{3 } } = x](_images/math/b1b2175a753761cdbee2007be016dd67d4053b84.png) per le radici cubiche non si deve mettere il valore assoluto
per le radici cubiche non si deve mettere il valore assoluto
![\sqrt[3 ]{x ^{3 } + 3x ^{2 } + 3x + 1 } = \sqrt[3 ]{( x + 1 ) ^{3 } } =
x + 1](_images/math/a06e31ac253bef8228419dfdc72724696d0a0251.png) non si deve mettere il valore assoluto
non si deve mettere il valore assoluto
Osserva che la radice cubica di un numero mantiene sempre lo stesso segno del numero in quanto il cubo di un numero reale conserva sempre il segno della base.
Radici n-esime¶
Oltre alle radici quadrate e cubiche si possono considerare radici di indice qualsiasi. Si parla in generale di radice n-esima per indicare una radice con un qualsiasi indice n.
DEFINIZIONE. Si dice radice n-esima di un numero reale
 quel numero
quel numero
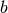 che elevato ad
che elevato ad
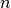 dà come risultato
dà come risultato
 .
.
In simboli
![\sqrt[n ]{a } = b \Leftrightarrow b ^{n } = a](_images/math/376a1162eda2cd35eea12a630f9e59e80cc511e6.png) con
con
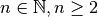 .
.
Non si definisce la radice di indice
 : la scrittura
: la scrittura
![\sqrt[0 ]{a }](_images/math/2a549a352af75542ef28ff9535944d01162b847c.png) è priva di significato.
è priva di significato.
Alla scrittura
![\sqrt[1 ]{a }](_images/math/0fd5abf4e9e8ae7746e91ce5dd789c4f4b5a8cce.png) si dà il valore a.
si dà il valore a.
Quando si tratta con le radici n-esime di un numero reale, bisogna fare attenzione se l’indice della radice è pari o dispari. Si presentano infatti i seguenti casi:
se l’indice n è dispari
![\sqrt[n ]{a }](_images/math/ec16c1b2a0b1fdca68eb9ef63e0ca8f1f5d2cf9d.png) è definita per qualsiasi valore di
è definita per qualsiasi valore di
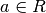 , inoltre è negativa se
, inoltre è negativa se
 , positiva se
, positiva se
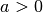 e nulla se
e nulla se
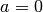 ;
;
se l’indice
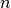 è pari
è pari
![\sqrt[n ]{a }](_images/math/ec16c1b2a0b1fdca68eb9ef63e0ca8f1f5d2cf9d.png) è definita solo per i valori di
è definita solo per i valori di
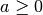 e si ha che
e si ha che
![\sqrt[n ]{a } \geq 0](_images/math/73703f9709f5aa47e57536b6bde08b5e8de992a2.png) .
.
Esempi
![\sqrt[4 ]{16 } = 2](_images/math/9f80e3af1a362be0f1fbc255e4a81f83a928d71c.png) infatti
infatti
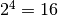
![\sqrt[4 ]{- 16 }](_images/math/c3e04b265e252376d5d31cd3c78bce9415272781.png) non esiste infatti
non esiste infatti
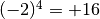
![\sqrt[5 ]{32 } = 2](_images/math/c41a4ae2af7cd679142244e5dfd8ac65413a3415.png) infatti
infatti
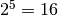
![\sqrt[4 ]{1 } = 1](_images/math/b80e822528c4a0845e6571136be9049e8737ac97.png) infatti
infatti
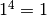
![\sqrt[n ]{0 } = 0](_images/math/5bcd9747c529dedbb9bac3eb5957eb4279f4001b.png)
![\sqrt[5 ]{- 1 } = - 1](_images/math/14b2ad8f6577a491c90420131cf5a92ebdb3d86b.png) infatti
infatti
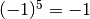
![\sqrt[4 ]{x ^{4 } } = \left\lvert x \right\rvert](_images/math/88c1b1f84469b54fa454addc4c18f79b3b72f10d.png) va messo il valore assoluto perché l’indice della radice è pari
va messo il valore assoluto perché l’indice della radice è pari
![\sqrt[5 ]{x ^{5 } } = x](_images/math/16eab8808f21ef9b7b87603cadd65d6ab2a77316.png) non va messo il valore assoluto perché l’indice della radice è dispari.
non va messo il valore assoluto perché l’indice della radice è dispari.
Condizioni di esistenza¶
Quando il radicando è un’espressione letterale dobbiamo fare molta attenzione a operare su di esso.
Le condizioni di esistenza, in breve si può scrivere C.E., di un radicale con radicando letterale, sono le condizioni cui devono soddisfare le variabili che compaiono nel radicando affinché la radice abbia significato.
Supponiamo di avere
![\sqrt[n ]{A ( x ) }](_images/math/90059ff3e124cd9f6a9c0d6d94ad8ebe091c0bc8.png) con A(x) polinomio nell’indeterminata x, dobbiamo distinguere i seguenti casi:
con A(x) polinomio nell’indeterminata x, dobbiamo distinguere i seguenti casi:
se n è pari la radice esiste per tutti i valori di x che rendono non negativo
il radicando, cioè C.E.
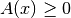
- se n è dispari la radice esiste per qualsiasi valore della variabile x, purché esista il radicando stesso.
Esempi
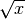 ;tab;C.E.
;tab;C.E.
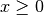 ,
,
![\sqrt[3 ]{x }](_images/math/0c7d1ddf7e6b1eea0466e95746ccdf5830ede90c.png) ;tab;C.E.
;tab;C.E.
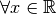
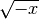 ;tab;C.E.
;tab;C.E.
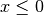
![\sqrt[3 ]{- x }](_images/math/41bca155d551302643ba926eab607c9b70543116.png) ;tab;C.E.
;tab;C.E.
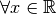
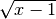 ;tab;C.E.
;tab;C.E.
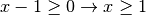
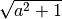 ;tab;C.E.
;tab;C.E.
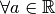 , infatti
, infatti
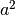 è sempre positivo pertanto
è sempre positivo pertanto
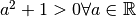
![\sqrt[3 ]{\frac{1 }{x + 1 } }](_images/math/549af8eba632dbea4433cdb94e812e08217c75d2.png) ;tab; C.E. La radice cubica è definita per valori sia positivi sia negativi
del radicando, tuttavia bisogna comunque porre la condizione che il
denominatore della frazione non sia nullo, quindi C.E.
;tab; C.E. La radice cubica è definita per valori sia positivi sia negativi
del radicando, tuttavia bisogna comunque porre la condizione che il
denominatore della frazione non sia nullo, quindi C.E.
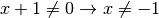 .
.
![\sqrt[4 ]{xy }](_images/math/780e030ca16c14a273078bf2e60f6177d83feec9.png) ;tab;C.E
;tab;C.E
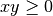
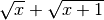 ;tab;C.E.
;tab;C.E.
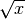 esiste per
esiste per
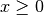 ,
,
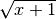 esiste per
esiste per
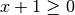 , per individuare le condizioni di esistenza dell’espressione occorre
risolvere il sistema
, per individuare le condizioni di esistenza dell’espressione occorre
risolvere il sistema
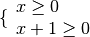 cioè
cioè
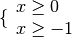
In definitiva C.E.
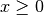 .
.
![\sqrt[4 ]{\frac{x - 1 }{x + 1 } }](_images/math/6b5ba602b25b262ab3df8559291ed5b6baaca414.png) ;tab;C.E.
;tab;C.E.
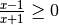 Occorre discutere il segno della frazione
Occorre discutere il segno della frazione
Pertanto C.E.
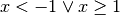
![\sqrt[5 ]{a ^{2 } ( a - 3 ) }](_images/math/f900ddcab8a9aad236c1fad6f8b20ba9257b556f.png) ;tab;Poiché la radice ha indice dispari non occorre porre alcuna condizione
di esistenza.
;tab;Poiché la radice ha indice dispari non occorre porre alcuna condizione
di esistenza.
Potenze a esponente razionale¶
In questo paragrafo ci proponiamo di scrivere la radice n-esima di un numero
reale
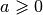 sotto forma di potenza di a, vogliamo cioè che sia:
sotto forma di potenza di a, vogliamo cioè che sia:
![\sqrt[n ]{a } = a ^{x }](_images/math/b1efc866a768f8e2f6307f65485bed8e9a4f1510.png)
Caso con esponente positivo¶
Elevando ambo i membri dell’uguaglianza alla potenza
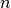 otteniamo:
otteniamo:
![\left( \sqrt[n ]{a } \right) ^{n } = \left( a ^{x } \right) ^{n }](_images/math/d4685c14b0d6e6f7777a65fabbc01230dc1954e3.png) da cui si ottiene
da cui si ottiene
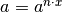
Trattandosi di due potenze con base
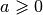 , l’uguaglianza è resa possibile solo se sono uguali gli esponenti. In altre
parole, deve essere:
, l’uguaglianza è resa possibile solo se sono uguali gli esponenti. In altre
parole, deve essere:
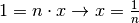
Possiamo quindi scrivere:
![\sqrt[n ]{a } = a ^{\frac{1 }{n } }](_images/math/96e5f8344fe86aac819877f0f504dde047e523b2.png)
Vediamo ora di generalizzare la formula. Sia m un numero intero positivo, possiamo scrivere
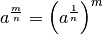
Pertanto possiamo scrivere che
![a ^{\frac{m }{n } } = \left( \sqrt[n ]{a } \right) ^{m }](_images/math/9a495231d0e73f7ab25ba93ea94066257186960c.png)
Esempi
Calcola
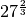 Si ha che
Si ha che
![27 ^{\frac{2 }{3 } } = \left( \sqrt[3 ]{27 } \right) ^{2 } = 3 ^{2 } =
9](_images/math/c939181223a53010ca33e629b2c4d6ab59acd3ab.png)
Calcola
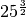 Si ha che
Si ha che
![25 ^{\frac{3 }{2 } } = \left( \sqrt[2 ]{25 } \right) ^{3 } = 5 ^{3 } =
125](_images/math/ca20d30d303061a2a2606617cf7f023737133805.png)
Caso con esponente negativo¶
Per definire la potenza ad esponente razionale negativo è necessario imporre la
restrizione
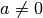 , infatti risulta:
, infatti risulta:
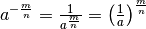
Esempi
![27 ^{- \frac{2 }{3 } } = \frac{1 }{\left( \sqrt[3 ]{27 } \right) ^{2 }
} = \frac{1 }{3 ^{2 } } = \frac{1 }{9 }](_images/math/4dbd3d55b0356cb4fc6473f08d2f62a503f4ffad.png)
![125 ^{- \frac{2 }{3 } } = \sqrt[3 ]{125 ^{- 2 } } = \sqrt[3 ]{( 5 ^{3 }
) ^{- 2 } } = \sqrt[3 ]{( 5 ^{- 2 } ) ^{3 } } = 5 ^{- 2 } = \frac{1 }{25 }](_images/math/6914779e16524bda16a972e10fa9f2ac83dc22fa.png)
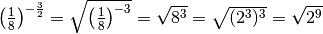
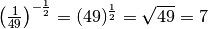
In generale si dà la seguente
DEFINIZIONE. Si dice potenza a esponente razionale
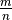 di un numero reale positivo
di un numero reale positivo
 l’espressione:
l’espressione:
![a ^{\frac{m }{n } } = \sqrt[n ]{a ^{m } } = \left( \sqrt[n ]{a } \right)
^{m }](_images/math/bb8f2ecf1d6cf13ffe49f0364fbef58cd65264a0.png) con
con
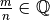
Perché abbiamo dovuto imporre la condizione che
 sia un numero positivo?
sia un numero positivo?
Partiamo dall’espressione
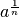 con
con
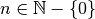 , se n è dispari la potenza
, se n è dispari la potenza
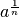 è sempre definita per ogni valore della base
è sempre definita per ogni valore della base
 , mentre se è pari
, mentre se è pari
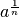 è definita solo per
è definita solo per
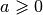 .
.
Nel caso generale
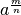 con
con
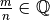 la formula
la formula
![a ^{\frac{m }{n } } = \left( \sqrt[n ]{a } \right) ^{m }](_images/math/9a495231d0e73f7ab25ba93ea94066257186960c.png) è falsa se
è falsa se
 .
.
Infatti facciamo un esempio:
![( - 2 ) ^{\frac{6 }{6 } } = \left\{ ( - 2 ) ^{\frac{1 }{6 } } \right\}
^{6 } = \left( \sqrt[6 ]{- 2 } \right) ^{6 }](_images/math/0117ad11ec36b6cbe26902b545b0924ef008ba1c.png) che non è definita nei numeri reali perché non esiste la radice sesta di un
numero negativo.
che non è definita nei numeri reali perché non esiste la radice sesta di un
numero negativo.
Tuttavia possiamo anche scrivere
![( - 2 ) ^{\frac{6 }{6 } } = \left\{ ( - 2 ) ^{6 } \right\} ^{\frac{1 }{6
} } = ( 64 ) ^{\frac{1 }{6 } } = \sqrt[6 ]{64 } = 2](_images/math/2815ef2c2c62229e87ac7f1e6674463613f67a34.png)
Arriviamo pertanto a due risultati differenti.
Per estendere la definizione al caso di basi negative sarebbe necessario stabilire un ordine di priorità delle operazioni ma ciò andrebbe contro la proprietà commutativa del prodotto degli esponenti di una potenza di potenza.
Semplificazione delle radici¶
PROPOSIZIONE. Il valore di una radice in
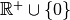 non cambia se moltiplichiamo l’indice della radice e l’esponente del radicando
per uno stesso numero intero positivo.
non cambia se moltiplichiamo l’indice della radice e l’esponente del radicando
per uno stesso numero intero positivo.
In simboli
![\sqrt[n ]{a ^{m } } = \sqrt[nt ]{a ^{mt } }](_images/math/568fca05aa02efa3519e4aa8dc3f40464c81ad2d.png) con
con
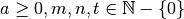
Esempi
![\sqrt{2 } = \sqrt[4 ]{2 ^{2 } }](_images/math/e28430e63374485b7dd34d50ad75b2d3607a958e.png) abbiamo moltiplicato per 2 indice della radice ed esponente del radicando.
abbiamo moltiplicato per 2 indice della radice ed esponente del radicando.
![\sqrt[3 ]{a } = \sqrt[9 ]{a ^{3 } }](_images/math/c6d19ceefe94d9e5356fb77113bdbe2efffcc193.png) abbiamo moltiplicato per 3 indice della radice ed esponente del radicando
abbiamo moltiplicato per 3 indice della radice ed esponente del radicando
PROPOSIZIONE. Il valore di una radice in
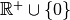 non cambia se dividiamo l’indice della radice e l’esponente del radicando per un
loro divisore comune.In simboli
non cambia se dividiamo l’indice della radice e l’esponente del radicando per un
loro divisore comune.In simboli
![\sqrt[nt ]{a ^{mt } } = \sqrt[n ]{a ^{m } }](_images/math/24ba2dd7c9e4c18ccff5f20079b67eeefcede8e6.png) con
con
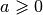
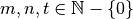
Esempi
![\sqrt[4 ]{2 ^{2 } } = \sqrt{2 }](_images/math/1ed7567032d23a52081f692c32cddb79358bfeb8.png) abbiamo semplificato per 2 indice della radice ed esponente del radicando.
abbiamo semplificato per 2 indice della radice ed esponente del radicando.
![\sqrt[10 ]{3 ^{15 } } = \sqrt{3 ^{3 } }](_images/math/4562119b49886a3fd5e908415859ba68b9bde12a.png) abbiamo semplificato per 5.
abbiamo semplificato per 5.
![\sqrt[7 ]{3 ^{9 } }](_images/math/1d6d16c89fc6abc3a40dd90028dd4ba27e97595c.png) non è riducibile perché indice della radice ed esponente non hanno divisori
comuni.
non è riducibile perché indice della radice ed esponente non hanno divisori
comuni.
![\sqrt[8 ]{2 ^{6 } } = 2 ^{\frac{6 }{8 } } =](_images/math/8a819cf7fdc4cf4ba795857c53fcd33f9f0da1e4.png) semplificando la frazione dell’esponente
semplificando la frazione dell’esponente
![= 2 ^{\frac{3 }{4 } } = \sqrt[4 ]{2 ^{3 } }](_images/math/c67f88036ffe60f52ae0161b9f13579d8faa292c.png)
![\sqrt[6 ]{\left( \frac{1 }{5 } \right) ^{- 9 } } = \sqrt[6 ]{5 ^{9 } }
= \sqrt[2 ]{5 ^{3 } }](_images/math/3aab1327ad303ab2f57bed68625f7d4ec7ebab28.png)
![\sqrt[4 ]{( - 3 ) ^{2 } } = \sqrt[4 ]{3 ^{2 } } = \sqrt{3 }](_images/math/c4e3fdcc7f485e21cf28e544358bafac0a4770f0.png)
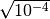 semplificando per 2 indice della radice ed esponente del radicando si ha
semplificando per 2 indice della radice ed esponente del radicando si ha
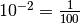
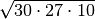 scomponendo in fattori primi otteniamo
scomponendo in fattori primi otteniamo
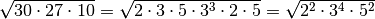 osserviamo che tutti gli esponenti del radicando e l’indice della radice hanno
un divisore, quindi
osserviamo che tutti gli esponenti del radicando e l’indice della radice hanno
un divisore, quindi
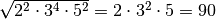
Se il radicando è un’espressione letterale, quindi sia positiva che negativa,
dobbiamo scrivere
![\sqrt[nt ]{a ^{mt } } = \left \{ \begin{array}{l } \sqrt[n ]{a ^{m } }
\text{ se la potenza t che abbiamo semplificato è dispari} \\\sqrt[n
]{\left\lvert a ^{m } \right\rvert } \text{ se t è pari} \end{array}\right
.](_images/math/f485004ac5cc587e3cf4f93fb05e5fe0cf616d65.png)
Esempi
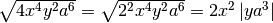 abbiamo semplificato per 2 sia l’indice della radice che l’esponente del
radicando.
abbiamo semplificato per 2 sia l’indice della radice che l’esponente del
radicando.
![\sqrt[12 ]{a ^{2 } + 2a + 1 } = \sqrt[12 ]{( a + 1 ) ^{2 } } = \sqrt[6
]{\left\lvert a + 1 \right\rvert }](_images/math/795d536a569f3b09a788be27fa20f0bd01d992eb.png) Dopo aver riconosciuto che il radicando è il quadrato del binomio, abbiamo
semplificato per 2 gli indici.
Dopo aver riconosciuto che il radicando è il quadrato del binomio, abbiamo
semplificato per 2 gli indici.
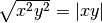 ;
;
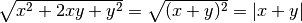 ;
;
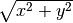 non è semplificabile perché il radicando non può essere espresso sotto
forma di potenza.
non è semplificabile perché il radicando non può essere espresso sotto
forma di potenza.
![\sqrt[6 ]{( x - 1 ) ^{2 } } = \sqrt[3 ]{\left\lvert x - 1 \right\rvert
}](_images/math/382385f2cf0396db1b3605ad5feac1244cf94b55.png)
La proprietà invariantiva si può applicare per semplificare i radicali se la
base del radicando è positiva o nulla, se fosse negativa si potrebbe perdere la
concordanza del segno. Per esempio
![\sqrt[10 ]{( - 2 ) ^{6 } } \neq \sqrt[5 ]{( - 2 ) ^{3 } }](_images/math/80969b92bade48ce6fbe0577f500c2dc2964c303.png) infatti il primo radicando è positivo mentre il secondo è negativo.
infatti il primo radicando è positivo mentre il secondo è negativo.
Invece
![\sqrt[9 ]{( - 2 ) ^{3 } } = \sqrt[3 ]{- 2 }](_images/math/5d96faea60de9b4aae5d4138480b5f227576b144.png) perché in questo caso la concordanza del segno è conservata, infatti pur
essendo la base negativa, l’esponente resta dispari, conservando il segno
della base.
perché in questo caso la concordanza del segno è conservata, infatti pur
essendo la base negativa, l’esponente resta dispari, conservando il segno
della base.
Se il radicando ha base negativa e nella semplificazione il suo esponente passa
da pari a dispari è necessario mettere il radicando in valore assoluto:
![\sqrt[10 ]{( - 2 ) ^{6 } } = \sqrt[5 ]{\left\lvert - 2 ^{3 }
\right\rvert }](_images/math/3291103a61c1bfdc3c27d543ebe95b512c980748.png) .
.
Se il radicando è letterale si segue la stessa procedura: ogni volta che
studiando il segno del radicando si trova che la base può essere negativa, se
l’esponente del radicando passa da pari a dispari, si mette il modulo per
garantire la concordanza del segno:
![\sqrt[10 ]{x ^{6 } } = \sqrt[5 ]{\left\lvert x ^{3 } \right\rvert }](_images/math/588284129e92cb14a2154f5aad87d9174b7605f2.png) C.E: x può assumere qualunque valore reale.
C.E: x può assumere qualunque valore reale.
Moltiplicazione e divisione di radici¶
Prima di operare con i radicali letterali, è necessario determinare le condizioni di esistenza: il prodotto di due radicali esiste là dove sono soddisfatte le condizioni di esistenza di tutti i fattori; il quoziente esiste là dove sono soddisfatte le condizioni di esistenza di dividendo e divisore, con il divisore diverso da zero.
Moltiplicazione e divisione di radici con lo stesso radicando¶
Per effettuare la moltiplicazione o la divisione tra radici aventi lo stesso radicando si possono trasformare le radici in forma di potenze con esponente razionale e utilizzare le proprietà delle potenze.
Esempi
![\sqrt[4 ]{6 } \cdot \sqrt[3 ]{6 } = 6 ^{\frac{1 }{4 } } \cdot 6
^{\frac{1 }{3 } } = 6 ^{\frac{1 }{4 } + \frac{1 }{3 } } = 6 ^{\frac{7 }{12 } }
= \sqrt[12 ]{6 ^{7 } }](_images/math/0ae20cc9895bfe25d05e97abd09dc99992a24a7a.png)
![\sqrt[4 ]{6 } \div \sqrt[3 ]{6 } = 6 ^{\frac{1 }{4 } } \div 6
^{\frac{1 }{3 } } = 6 ^{\frac{1 }{4 } - \frac{1 }{3 } } = 6 ^{- \frac{1 }{12 }
} = \frac{1 }{\sqrt[12 ]{6 } }](_images/math/562751735bd3a455307ad9ed9574195ee8a99564.png)
Moltiplicazione e divisione di radici con lo stesso indice¶
Il prodotto di due radici che hanno lo stesso indice è una radice che ha per indice lo stesso indice e per radicando il prodotto dei radicandi:
![\sqrt[n ]{a } \cdot \sqrt[n ]{b } = \sqrt[n ]{ab }](_images/math/84ea959e7144fbe2072fe0bed7b7e7cc04d94d53.png)
Allo stesso modo, il quoziente di due radici che hanno lo stesso indice è una radice che ha per indice lo stesso indice e per radicando il quoziente dei radicandi:
![\sqrt[n ]{a } \div \sqrt[n ]{b } = \sqrt[n ]{a \div b } \rightarrow
\frac{\sqrt[n ]{a } }{\sqrt[n ]{b } } = \sqrt[n ]{\frac{a }{b } }](_images/math/7b3e1311e67866f8581e028fa559e7666bf56f1a.png)
Anche per rendersi conto di questa proprietà si possono trasformare le radici in potenze ad esponenti razionali e applicare le proprietà delle potenze:
![\sqrt[n ]{a } \cdot \sqrt[n ]{b } = a ^{\frac{1 }{n } } \cdot b ^{\frac{1
}{n } } = ( ab ) ^{\frac{1 }{n } } = \sqrt[n ]{ab } \rightarrow \sqrt[n ]{a
} \div \sqrt[n ]{b } = a ^{\frac{1 }{n } } \div b ^{\frac{1 }{n } } = \left(
\frac{a }{b } \right) ^{\frac{1 }{n } } = \sqrt[n ]{\frac{a }{b } }](_images/math/c219a542e40d072764230213a954bc806492198e.png)
Esempi
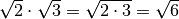
![\frac{\sqrt[3 ]{9 } }{\sqrt[3 ]{72 } } = \sqrt[3 ]{\frac{9 }{72 } } =
\sqrt[3 ]{\frac{1 }{8 } } = \frac{1 }{2 }](_images/math/b83da4f6056ad9ebacd44dc20f76f376623b58e4.png)
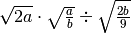 C.E.
C.E.
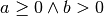
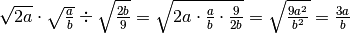
Moltiplicazione e divisione di radici con indici diversi¶
Per moltiplicare o dividere radici con indici differenti è necessario prima ridurre le radici allo stesso indice, cioè trasformarle in radici equivalenti con lo stesso indice usando la proprietà invariantiva. Dopo aver ottenuto radici con lo stesso indice si applica la regola precedente.
Procedura per ridurre due o più radici allo stesso indice:
- scomporre in fattori irriducibili tutti i radicandi;
- porre le condizioni di esistenza;
- calcolare il minimo comune multiplo tra gli indici delle radici;
- per ciascuna radice dividere il m.c.m. per l’indice della radice e moltiplicare il quoziente trovato per l’esponente del radicando.
Esempi
![\sqrt{2 } \cdot \sqrt[3 ]{2 }](_images/math/c632a1b0aded4c1be243c847dd2024724bb48e76.png) Gli indici delle radici sono 2 e 3, il loro m.c.m. è 6, il primo radicando va
elevato a 6:2 cioè 3, mentre il secondo radicando va elevato a 6:3 cioè 2
Gli indici delle radici sono 2 e 3, il loro m.c.m. è 6, il primo radicando va
elevato a 6:2 cioè 3, mentre il secondo radicando va elevato a 6:3 cioè 2
![\sqrt{2 } \cdot \sqrt[3 ]{2 } = \sqrt[6 ]{2 ^{3 } } \cdot \sqrt[6 ]{2
^{2 } } = \sqrt[6 ]{2 ^{3 } \cdot 2 ^{2 } } = \sqrt[6 ]{2 ^{5 } }](_images/math/c2ae0598427d7e969af5c43c02437d591b40a8b6.png)
![\sqrt[3 ]{\frac{3 }{2 } } \cdot \sqrt[4 ]{\frac{8 }{27 } } \div
\sqrt[6 ]{\frac{2 }{3 } }](_images/math/ac8ad3e65f4128258f51b8f50bd6f33fda0249a8.png) Il m.c.m. tra gli indici delle radici è 12. Il primo radicando va elevato a
12:3=4; il secondo radicando va elevato a 12:4=3; il terzo va elevato a
12:6=2.
Il m.c.m. tra gli indici delle radici è 12. Il primo radicando va elevato a
12:3=4; il secondo radicando va elevato a 12:4=3; il terzo va elevato a
12:6=2.
![\sqrt[3 ]{\frac{3 }{2 } } \cdot \sqrt[4 ]{\frac{8 }{27 } } \div
\sqrt[6 ]{\frac{2 }{3 } } = \sqrt[12 ]{\frac{3 ^{4 } }{2 ^{4 } } \cdot \frac{8
^{3 } }{27 ^{3 } } \div \frac{2 ^{2 } }{3 ^{2 } } } = \sqrt[12 ]{\frac{3 ^{4
} }{2 ^{4 } } \cdot \frac{( 2 ^{3 } ) ^{3 } }{( 3 ^{3 } ) ^{3 } } \div
\frac{2 ^{2 } }{3 ^{2 } } } = \sqrt[12 ]{\frac{3 ^{4 } }{2 ^{4 } } \cdot
\frac{2 ^{9 } }{3 ^{9 } } \div \frac{2 ^{2 } }{3 ^{2 } } } = \sqrt[12
]{\frac{3 ^{6 } \cdot 2 ^{9 } }{3 ^{9 } \cdot 2 ^{6 } } } = \sqrt[12 ]{\frac{2
^{3 } }{3 ^{3 } } } = \sqrt[4 ]{\frac{2 }{3 } }](_images/math/4cf713b6a53d7bd860090271f1b1ae890ec74858.png)
![\frac{\sqrt[3 ]{x ^{2 } y } \cdot \sqrt{xy } }{\sqrt[6 ]{x ^{2 } y ^{3
} } }](_images/math/876bc8761848bf308b200bb313133c84a0b85254.png) C.E.
C.E.
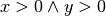 . Il m.c.m. degli indici delle radici è 6, quindi:
. Il m.c.m. degli indici delle radici è 6, quindi:
![\frac{\sqrt[3 ]{x ^{2 } y } \cdot \sqrt{xy } }{\sqrt[6 ]{x ^{2 } y ^{3
} } } = \sqrt[6 ]{\frac{\left( x ^{2 } y \right) ^{2 } \cdot \left( xy
\right) ^{3 } }{x ^{2 } y ^{3 } } } = \sqrt[6 ]{\frac{x ^{4 } y ^{2 } x ^{3 }
y ^{3 } }{x ^{2 } y ^{3 } } } = \sqrt[6 ]{\frac{x ^{7 } y ^{5 } }{x ^{2 } y
^{3 } } } = \sqrt[6 ]{x ^{5 } y ^{2 } }](_images/math/53bcd9e0b204f4540003bf26178f7dc433a71e72.png)
![\sqrt[3 ]{\frac{a x + a }{x ^{2 } + 2 x + 1 } } \cdot \sqrt{\frac{x ^{2
} - 2 x + 1 }{a x - a } }](_images/math/ccdec50efbd8ad496ad1130d7e9c1a2e535d0a62.png)
Scomponiamo in fattori i radicandi
![\sqrt[3 ]{\frac{a ( x + 1 ) }{( x + 1 ) ^{2 } } } \cdot \sqrt{\frac{( x
- 1 ) ^{2 } }{a ( x - 1 ) } }](_images/math/40b26c06404ae674a978f0f91e53f8753a849216.png)
Poniamo le C.E.
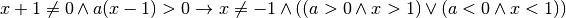
Semplifichiamo le frazioni di ciascun radicando
![\sqrt[3 ]{\frac{a }{x + 1 } } \cdot \sqrt{\frac{x - 1 }{a } }](_images/math/766c2dadb643e54e1fa0e8605da4578739d1a464.png)
- Trasformiamo nello stesso indice: il m.c.m. degli indici è 6, quindi
![\sqrt[6 ]{\left( \frac{a }{x + 1 } \right) ^{2 } } \cdot \sqrt[6
]{\left( \frac{x - 1 }{a } \right) ^{3 } } = \sqrt[6 ]{\frac{a ^{2 } }{( x +
1 ) ^{2 } } \cdot \frac{( x - 1 ) ^{3 } }{a ^{3 } } } = \sqrt[6 ]{\frac{( x -
1 ) ^{3 } }{a ( x + 1 ) ^{2 } } }](_images/math/d604af133a3e162a3232dfd66c31d60c0591726f.png)
![\sqrt[3 ]{\frac{x ^{2 } }{x ^{2 } - 2 x + 1 } } \div \sqrt[4 ]{\frac{x
^{4 } - 2 x ^{2 } + 1 }{x ^{2 } - 1 } }](_images/math/7a6b0bfd3d37b689e6a2169f9321558875916285.png)
Scomponiamo in fattori i radicandi
Determiniamo le C.E.
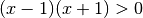
. L’operazione che dobbiamo eseguire è una divisione e dunque il divisore deve essere diverso da zero, quindi
, comunque già implicite nelle C.E. trovate
Semplifichiamo i radicandi
Riduciamo allo stesso indice: il m.c.m. degli indici è 12
Poniamo sotto la stessa radice
.
Portare un fattore sotto il segno di radice¶
Per portare un fattore dentro il segno di radice bisogna elevarlo all’indice della radice:
![a \sqrt[n ]{b } = \sqrt[n ]{a ^{n } \cdot b }](_images/math/d0f35f4f0ca93ea7667b49b798a208d28bc70e43.png) se n pari e
se n pari e
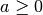
![a \sqrt[n ]{b } = - \sqrt[n ]{a ^{n } \cdot b }](_images/math/b329b4f3c36c38828a632b09de77c65c40196df0.png) se n pari e
se n pari e

![a \sqrt[n ]{b } = \sqrt[n ]{a ^{n } \cdot b }](_images/math/d0f35f4f0ca93ea7667b49b798a208d28bc70e43.png) se n dispari
se n dispari
Ricordando che abbiamo posto
![\sqrt[1 ]{a } = a](_images/math/14e4f37d629ab52619a4dcf1640aa0086d783ff6.png) , portare un fattore sotto radice equivale a svolgere la moltiplicazione tra una
radice di indice 1 e una radice di indice qualsiasi.
, portare un fattore sotto radice equivale a svolgere la moltiplicazione tra una
radice di indice 1 e una radice di indice qualsiasi.
Esempi
![2 \sqrt[3 ]{5 }](_images/math/43d7219531dd2d9786a110369bf05aaaf066c0a5.png) portare il 2 dentro il segno di radice;tab;
portare il 2 dentro il segno di radice;tab;
![2 \sqrt[3 ]{5 } = \sqrt[3 ]{2 ^{3 } \cdot 5 } = \sqrt[3 ]{40 }](_images/math/4057b61257b6bed7a51fa3d9705855671bf87cb3.png)
![2 \cdot \sqrt[3 ]{7 } = \sqrt[3 ]{2 ^{3 } \cdot 7 } = \sqrt[3 ]{56 }](_images/math/dd499d18d79756f8ef4fb497f406d33b26bf3c3d.png)
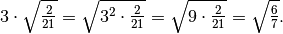
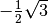 lasciamo fuori dalla radice il segno meno
lasciamo fuori dalla radice il segno meno
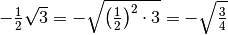
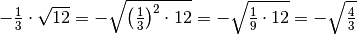
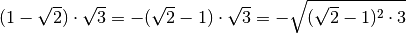
![- 2 \sqrt[3 ]{5 } = \sqrt[3 ]{( - 2 ) ^{3 } \cdot 5 } = \sqrt[3 ]{- 40
}](_images/math/5a9ef315c04779fab6cab2dab24544d7adabbfc0.png)
![a \cdot \sqrt[3 ]{b } = \sqrt[3 ]{a ^{3 } b }](_images/math/6c9fc8260378d9a6233e76041c7d69b3a96f9861.png) l’indice della radice è dispari pertanto si porta sotto radice senza alcuna
condizione.
l’indice della radice è dispari pertanto si porta sotto radice senza alcuna
condizione.
![( x - 1 ) \cdot \sqrt[3 ]{x } = \sqrt[3 ]{( x - 1 ) ^{3 } \cdot x }](_images/math/14cae645fceea9aaa50f23c7664290a3c048a69b.png) l’indice della radice è dispari, non sono necessarie condizioni sulla x.
l’indice della radice è dispari, non sono necessarie condizioni sulla x.
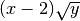 osserviamo che il radicale esiste per
osserviamo che il radicale esiste per
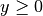 .Per portare dentro il segno di radice il coefficiente (x-2) bisogna fare la
distinzione:
.Per portare dentro il segno di radice il coefficiente (x-2) bisogna fare la
distinzione:
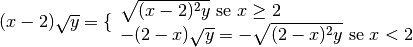
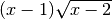 Il radicale esiste per
Il radicale esiste per
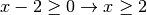 , per questi valori il coefficiente esterno (x-1) è positivo e può essere
portato dentro la radice
, per questi valori il coefficiente esterno (x-1) è positivo e può essere
portato dentro la radice
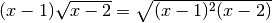 .
.
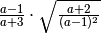 Determiniamo le condizioni di esistenza del radicale. Per l’esistenza della
frazione
Determiniamo le condizioni di esistenza del radicale. Per l’esistenza della
frazione
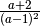 deve essere
deve essere
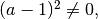 ovvero
ovvero
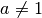 . Affinché il radicando sia positivo o nullo, essendo il denominatore sempre
positivo (ovviamente per
. Affinché il radicando sia positivo o nullo, essendo il denominatore sempre
positivo (ovviamente per
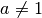 ) è sufficiente che sia
) è sufficiente che sia
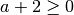 ovvero
ovvero
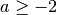 . Pertanto le condizioni di esistenza sono
. Pertanto le condizioni di esistenza sono
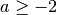 e
e
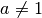 .Studiamo il segno della frazione algebrica da portare sotto radice. Tale
frazione è positiva o nulla per
.Studiamo il segno della frazione algebrica da portare sotto radice. Tale
frazione è positiva o nulla per
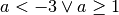 , è negativa per
, è negativa per
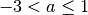 .
.
Se
si ha
Se
il fattore da portare sotto radice è negativo, quindTrasporta dentro la radice i fattori esterni, discutendo i casi letterali
Se
l’espressione da calcolare vale zero, mentre Il caso
è escluso dalla condizione di esistenza.
Portare uno o più fattori fuori dal segno di radice¶
È possibile portare fuori dal segno di radice quei fattori aventi come
esponente un numero che sia maggiore o uguale all’indice della radice. In
generale si inizia scomponendo in fattori irriducibili il radicando, ottenendo
un radicale del tipo
![\sqrt[n ]{a ^{m } }](_images/math/eb4ee8f7a1b3dfe0079aebc9fd1c434559b78bc9.png) con
con
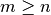
I° modo
Si esegue la divisione itera
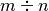 ottenendo un quoziente
ottenendo un quoziente
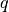 e un resto
e un resto
 . Per la proprietà della divisione si ha
. Per la proprietà della divisione si ha
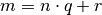 quindi il radicale diventa
quindi il radicale diventa
![\sqrt[n ]{a ^{m } }](_images/math/eb4ee8f7a1b3dfe0079aebc9fd1c434559b78bc9.png) , per le proprietà delle potenze il radicando si trasforma in un prodotto di
potenze
, per le proprietà delle potenze il radicando si trasforma in un prodotto di
potenze
![\sqrt[n ]{a ^{n \cdot q + r } } = \sqrt[n ]{( a ^{q } ) ^{n } \cdot a ^{r
} }](_images/math/bd4d5fb1394246e557995b38140ba81bab4ff2b9.png) e per la regola del prodotto di due radici con medesimo indice si ottiene
e per la regola del prodotto di due radici con medesimo indice si ottiene
![\sqrt[n ]{a ^{n \cdot q + r } } = \sqrt[n ]{( a ^{q } ) ^{n } \cdot a ^{r
} } = \sqrt[n ]{( a ^{q } ) ^{n } } \cdot \sqrt[n ]{a ^{r } } = a ^{q } \cdot
\sqrt[n ]{a ^{r } }](_images/math/0f820c478c51a9df97b9b5f7939add566015093c.png) con
con
 . Notiamo che nella divisione intera e sotto la radice lo stesso fattore
. Notiamo che nella divisione intera e sotto la radice lo stesso fattore
 con l’esponente uguale al resto della divisione.
con l’esponente uguale al resto della divisione.
Esempio
![\sqrt[3 ]{a ^{8 } } = \ldots](_images/math/4a3460e0f8997ec4bdea58e29c3758f48557a9ca.png) eseguiamo la divisione
eseguiamo la divisione
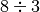 con
con
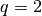 e
e
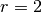 , otteniamo
, otteniamo
![\sqrt[3 ]{a ^{8 } } = a ^{2 } \cdot \sqrt[3 ]{a ^{2 } }](_images/math/8f55bcc697bf4aa621451fd6ef55b1a8b9efd580.png)
II° modo
Si può trasformare la potenza del radicando nel prodotto di due potenze con la stessa base; una avente esponente multiplo dell’indice della radice e l’altra avente per esponente la differenza tra l’esponente iniziale e il multiplo trovato.
Esempi
![\sqrt[3 ]{a ^{8 } } = \ldots](_images/math/4a3460e0f8997ec4bdea58e29c3758f48557a9ca.png) il multiplo di 3 più vicino a 8 è 6 quindi , otteniamo
il multiplo di 3 più vicino a 8 è 6 quindi , otteniamo
![\sqrt[3 ]{a ^{8 } } = \sqrt[3 ]{a ^{6 } \cdot a ^{2 } } = \sqrt[3 ]{a
^{6 } } \cdot \sqrt[3 ]{a ^{2 } } = a ^{2 } \cdot \sqrt[3 ]{a ^{2 } }](_images/math/9951ba33b6f9b0b4a6f49fe8aa44bccb9f827549.png)
![\sqrt[3 ]{a ^{5 } } = \sqrt[3 ]{a ^{3 } \cdot a ^{2 } } = \sqrt[3 ]{a
^{3 } } \cdot \sqrt[3 ]{a ^{2 } } = a \sqrt[3 ]{a ^{2 } }](_images/math/aee8c40e322a4f7381ae104b07607be2dda95087.png)
Quando portiamo fuori dalla radice un termine letterale dobbiamo verificare se l’indice della radice è pari o dispari e se il termine che portiamo fuori è positivo o negativo. In particolare
![\sqrt[n ]{a ^{n } b } = \{ \begin{array}{l } a \sqrt[n ]{b } \text{ se
} n \text{ dispari} \\\left\lvert a \right\rvert \sqrt[n ]{b } \text{ se } n
\text{ pari} \end{array}](_images/math/2888e0d3943176e4d65338b017e12153a30a227d.png)
Esempi
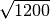 Si scompone in fattori primi il radicando
Si scompone in fattori primi il radicando
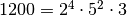 ne segue allora che
ne segue allora che
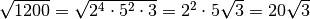
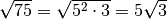
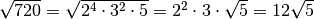
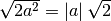 bisogna mettere
bisogna mettere
 in valore assoluto perché sotto radice poteva essere sia negativo che
positivo, la radice invece deve essere sempre positiva; se
in valore assoluto perché sotto radice poteva essere sia negativo che
positivo, la radice invece deve essere sempre positiva; se
 la relazione
la relazione
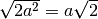 è errata
è errata
![\sqrt[3 ]{a ^{5 } b ^{7 } c d ^{3 } }](_images/math/d072aeff1d1fb35434d93d73d280945d28c392bb.png) Occorre eseguire le divisioni intere tra gli esponenti e l’indice della
radice. Cominciamo da
Occorre eseguire le divisioni intere tra gli esponenti e l’indice della
radice. Cominciamo da
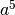 risulta 5:3 = quoziente 1, resto 2; per
risulta 5:3 = quoziente 1, resto 2; per
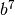 si ha 7:3 = quoziente 2, resto 1; l’esponente di
si ha 7:3 = quoziente 2, resto 1; l’esponente di
 è minore dell’indice; per
è minore dell’indice; per
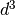 si ha 3:3= quoziente 1, resto 0. In definitiva
si ha 3:3= quoziente 1, resto 0. In definitiva
![\sqrt[3 ]{a ^{5 } b ^{7 } c d ^{3 } } = ab ^{2 } d \sqrt[3 ]{a ^{2 } bc
}](_images/math/2761d22b80e8e59efdb4e5ee366749529fdd2ea2.png) , o anche:
, o anche:
![\sqrt[3 ]{a ^{5 } b ^{7 } c d ^{3 } } = \sqrt[3 ]{( a ^{3 } a ^{2 } ) (
b ^{6 } b ) c d ^{3 } } = \sqrt[3 ]{a ^{3 } b ^{6 } d ^{3 } } \cdot \sqrt[3
]{a ^{2 } b c } = a b ^{2 } d ^{3 } \sqrt[3 ]{a ^{2 } b c }](_images/math/54a093171d1bbede1a6db62cc161f3896f9d8e67.png) . In questo caso non c’è da mettere il valore assoluto perché l’indice della
radice è dispari.
. In questo caso non c’è da mettere il valore assoluto perché l’indice della
radice è dispari.
![\sqrt[3 ]{\frac{3 ^{3 } x ^{3 } y }{z ^{6 } } }](_images/math/d300f7a395f8a33d9e9dd019b09ded6c0f65a659.png)
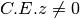
![\sqrt[3 ]{\frac{3 ^{3 } x ^{3 } y }{z ^{6 } } } = 3 \frac{x }{z ^{2 } }
\sqrt[3 ]{y }](_images/math/5d40b0364f04953de2352eccc45a6241304603d6.png)
![\sqrt[4 ]{4x ^{4 } - 4x ^{5 } }](_images/math/d42c09c84deaf6b4abd801cd67550a74b979e987.png) Scomponiamo il radicando per poter studiare le condizioni di esistenza del
radicale e portare fuori qualche fattore:
Scomponiamo il radicando per poter studiare le condizioni di esistenza del
radicale e portare fuori qualche fattore:
![\sqrt[4 ]{4x ^{4 } - 4x ^{5 } } = \sqrt[4 ]{4x ^{4 } ( 1 - x ) }](_images/math/68bd4f9f0d602edd1a04ad7868ac003f27056189.png) C.E.
C.E.
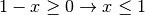 . Pertanto
. Pertanto
![\sqrt[4 ]{4x ^{4 } - 4x ^{5 } } = \sqrt[4 ]{4x ^{4 } ( 1 - x ) } =
\left\lvert x \right\rvert \sqrt[4 ]{4 ( 1 - x ) } = \left \{ \begin{array}{l
} x \sqrt[4 ]{4 ( 1 - x ) } \text{ se } 0 \leq x \leq 1 \\- x \sqrt[4 ]{4 (
1 - x ) } \text{ se } x < 0 \end{array}\right .](_images/math/01745e7893589ed076e31da243d2256b9c26254a.png)
 portare fuori dalla radice
portare fuori dalla radice
Potenza di radice e radice di radice¶
Potenza di radice¶
Per elevare a potenza una radice si eleva a quella potenza il radicando:
![\left( \sqrt[n ]{a } \right) ^{m } = \sqrt[n ]{a ^{m } }](_images/math/2cedb346527f1c69db5165658756b49d21c1bcc2.png) . Si capisce il perché di questa proprietà trasformando, come negli altri
casi, le radici in esponenti con indici frazionari:
. Si capisce il perché di questa proprietà trasformando, come negli altri
casi, le radici in esponenti con indici frazionari:
![\left( \sqrt[n ]{a } \right) ^{m } = \left( a ^{\frac{1 }{n } } \right)
^{m } = a ^{\frac{m }{n } } = \sqrt[n ]{a ^{m } }](_images/math/d1e3467dde133e5ae49844606d0e89afa0589afb.png)
Esempi
![\left( \sqrt[3 ]{2a b ^{2 } c ^{3 } } \right) ^{2 } = \sqrt[3 ]{4a ^{2
} b ^{4 } c ^{6 } }](_images/math/5d52cc349b61931d70cdbdd71822f431388f884d.png)
Radice di radice¶
La radice di un’altra radice è uguale a una radice con lo stesso radicando e
con indice il prodotto degli indici delle radici:
![\sqrt[m ]{\sqrt[n ]{a } } = \sqrt[m \cdot n ]{a }](_images/math/0b6ea977014267e666c1a7bf158f067adcf8f0e5.png) . Anche questa proprietà si può spiegare con le proprietà delle potenze
trasformando le radici in potenze con esponente frazionario:
. Anche questa proprietà si può spiegare con le proprietà delle potenze
trasformando le radici in potenze con esponente frazionario:
![\sqrt[m ]{\sqrt[n ]{a } } = \left( a ^{\frac{1 }{n } } \right) ^{\frac{1
}{m } } = a ^{\frac{1 }{mn } } = \sqrt[m \cdot n ]{a }](_images/math/c483a1f06060f3e949e0d1cc71b6d5f739e6541a.png)
Esempi
![\sqrt{\sqrt{2 } } = \sqrt[2 \cdot 2 ]{2 } = \sqrt[4 ]{2 }](_images/math/53001a47bbb669519f59012e3e563584bd28b318.png)
![\sqrt[3 ]{\sqrt[4 ]{2x } } = \sqrt[12 ]{2x }](_images/math/96caa8f31ee3cec04128dce63d2d74300b763f25.png)
Somma di radicali¶
Si dice radicale un’espressione del tipo
![a \sqrt[n ]{b }](_images/math/ad472a58f2f8e1077e944ea0175534be0da08317.png) con
con
 e
e
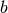 numeri reali,
numeri reali,
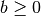 ed
ed
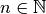 . Il numero
. Il numero
 prende il nome di coefficiente del radicale.
prende il nome di coefficiente del radicale.
Operare con i radicali è simile al modo di operare con i monomi. Infatti è possibile effettuare somme algebriche soltanto se i radicali hanno lo stesso indice e lo stesso radicando, mentre si possono sempre effettuare moltiplicazioni e divisioni dopo averli ridotti allo stesso indice.
DEFINIZIONE. Due radicali si dicono simili se hanno lo stesso indice e lo stesso radicando.
È possibile effettuare somme algebriche soltanto se i radicali sono simili, si eseguono le somme allo stesso modo in cui si eseguono le somme algebriche dei monomi.
Attenzione l’operazione
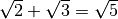 è errata: i radicali addendi non sono simili.
è errata: i radicali addendi non sono simili.
Esempi
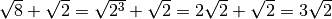
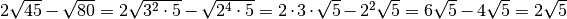 .
.
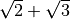 non si può eseguire perché i radicali non sono simili
non si può eseguire perché i radicali non sono simili
![\sqrt[3 ]{2 } + \sqrt{2 }](_images/math/d5d70094ec29c4669ea5a661a0662d77760f26c7.png) non si può eseguire perché i radicali non sono simili
non si può eseguire perché i radicali non sono simili
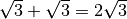
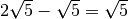
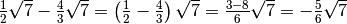
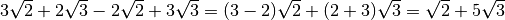 sommiamo i radicali simili
sommiamo i radicali simili
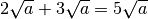 C.E.
C.E.
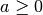
![\sqrt[4 ]{a ^{5 } } + \sqrt[4 ]{a ^{3 } } \cdot \sqrt{a } + \sqrt[4 ]{a
^{6 } } \div \sqrt[4 ]{a } = \sqrt[4 ]{a ^{5 } } + \sqrt[4 ]{a ^{3 } \cdot a
^{2 } } + \sqrt[4 ]{a ^{6 } \div a } = \sqrt[4 ]{a ^{5 } } + \sqrt[4 ]{a ^{5
} } + \sqrt[4 ]{a ^{5 } } = 3 \sqrt[4 ]{a ^{5 } } = 3 \sqrt[4 ]{a ^{4 } \cdot
a } = 3 a \sqrt[4 ]{a }](_images/math/82a4a1145aee632156edc5f70f509739d145d193.png) C.E.
C.E.
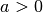
Per semplificare le espressioni che seguono, useremo le procedure di calcolo dei polinomi.
Esempi
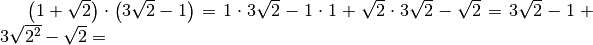
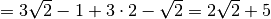
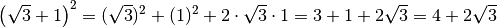
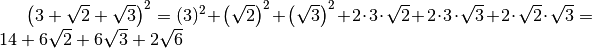
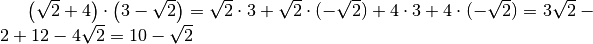
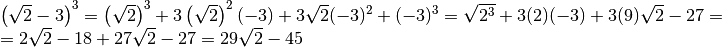
Le espressioni con radicali possono essere trasformate in potenze con esponente frazionario per poi applicare le proprietà delle potenze:
Esempi
![\frac{\sqrt{a } \cdot \sqrt[3 ]{a ^{2 } \cdot b } }{\sqrt[6 ]{a ^{5 }
\cdot b } } = \frac{a ^{\frac{1 }{2 } } \cdot a ^{\frac{2 }{3 } } \cdot b
^{\frac{1 }{3 } } }{a ^{\frac{5 }{6 } } \cdot b ^{\frac{1 }{6 } } } = a
^{\frac{1 }{2 } + \frac{2 }{3 } - \frac{5 }{6 } } \cdot b ^{\frac{1 }{3 } -
\frac{1 }{6 } } = a ^{\frac{2 }{6 } } \cdot b ^{\frac{1 }{6 } } = \sqrt[6 ]{a
^{2 } b }](_images/math/f6c623d6ff6931329ffbb3d8ffee25751c472f16.png)
![\sqrt{\frac{\sqrt[3 ]{a ^{2 } } \cdot \sqrt{b } }{\sqrt[5 ]{a ^{2 } } }
} \cdot \sqrt[3 ]{\frac{\sqrt[4 ]{a ^{6 } b } }{a \sqrt[3 ]{b } } } = \left(
\frac{a ^{\frac{2 }{3 } } \cdot b ^{\frac{1 }{2 } } }{a ^{\frac{2 }{5 } } }
\right) ^{\frac{1 }{2 } } \left( \frac{a ^{\frac{3 }{2 } } \cdot b ^{\frac{1
}{4 } } }{ab ^{\frac{1 }{3 } } } \right) ^{\frac{1 }{3 } } = \frac{a
^{\frac{1 }{3 } } \cdot b ^{\frac{1 }{4 } } }{a ^{\frac{1 }{5 } } } \cdot
\frac{a ^{\frac{1 }{2 } } \cdot b ^{\frac{1 }{12 } } }{a ^{\frac{1 }{3 } }
\cdot b ^{\frac{1 }{9 } } } = a ^{\frac{1 }{3 } - \frac{1 }{5 } + \frac{1
}{2 } - \frac{1 }{3 } } \cdot b ^{\frac{1 }{4 } + \frac{1 }{12 } - \frac{1 }{9
} } =](_images/math/01198882864a436e8a8d7ca9d7cb0d03b8607930.png)
![= a ^{\frac{3 }{10 } } \cdot b ^{\frac{2 }{9 } } = \sqrt[10 ]{a ^{3 } }
\cdot \sqrt[9 ]{b ^{2 } } .](_images/math/cdc479042d68e1bf9f7d728e26aadd36bfbc1218.png)
![\sqrt[6 ]{\frac{x ^{3 } \cdot \sqrt[3 ]{xy ^{2 } } }{x ^{2 } - \sqrt{xy
} } } = \left( \frac{x ^{3 } \cdot ( xy ^{2 } ) ^{\frac{1 }{3 } } }{x ^{2 } -
( xy ) ^{\frac{1 }{2 } } } \right) ^{\frac{1 }{6 } } = \left( \frac{x ^{3 }
\cdot x ^{\frac{1 }{3 } } \cdot y ^{\frac{2 }{3 } } }{x ^{2 } - x ^{\frac{1
}{2 } } \cdot y ^{\frac{1 }{2 } } } \right) ^{\frac{1 }{6 } } = \left(
\frac{x ^{\frac{10 }{3 } } \cdot y ^{\frac{2 }{3 } } }{x ^{\frac{1 }{2 } }
\cdot \left( x ^{\frac{3 }{2 } } - y ^{\frac{1 }{2 } } \right) } \right)
^{\frac{1 }{6 } } =](_images/math/4ed5f6b5174d50c85973c5588448c102879b57d7.png)
Razionalizzazione del denominatore di una frazione¶
Nel calcolo di espressioni che contengono radicali può capitare che al denominatore compaiano dei radicali. Per migliorare l’approssimazione si cerca di evitare questa situazione e operare affinché non compaiano radicali al denominatore. Questa operazione prende il nome di razionalizzazione del denominatore.
Razionalizzare il denominatore di una frazione vuol dire trasformare una frazione in una frazione equivalente avente per denominatore un’espressione nella quale non compaiano radici.
I Caso
La frazione è del tipo
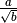
Per razionalizzare il denominatore di una frazione di questo tipo basta
moltiplicare numeratore e denominatore per
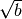 , che prende il nome di fattore razionalizzante:
, che prende il nome di fattore razionalizzante:
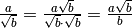
Esempi
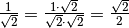
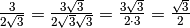
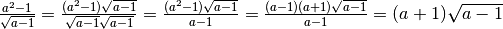
II Caso
La frazione è del tipo
![\frac{a }{\sqrt[n ]{b ^{m } } }](_images/math/9d831e54cb505b37ddba341f67528e9c053aac04.png) con
con
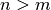 .
.
In questo caso il fattore razionalizzante è
![\sqrt[n ]{b ^{n - m } }](_images/math/927963f634642cb6333f19794000073dc652ae64.png) . Infatti si ha:
. Infatti si ha:
![\frac{a }{\sqrt[n ]{b ^{m } } } = \frac{a \sqrt[n ]{b ^{n - m } }
}{\sqrt[n ]{b ^{m } } \cdot \sqrt[n ]{b ^{( n - m ) } } } = \frac{a \sqrt[n ]{b
^{n - m } } }{\sqrt[n ]{b ^{m } \cdot b ^{n - m } } } = \frac{a \sqrt[n ]{b ^{n
- m } } }{\sqrt[n ]{b ^{n } } } = \frac{a \sqrt[n ]{b ^{n - m } } }{b }](_images/math/2df6f9717cd5c3cc3142fcf2548f0fb1dd4b8245.png)
Se abbiamo un esercizio in cui la potenza del radicando supera l’indice della radice, prima di razionalizzare possiamo portare fuori dalla radice.
Esempi
![\frac{1 }{\sqrt[3 ]{2 } }](_images/math/5ac1ff978587eaa4ce3f6c0338ebf00f77ffa8e7.png) il fattore razionalizzante è
il fattore razionalizzante è
![\sqrt[3 ]{2 ^{2 } }](_images/math/3deb136475f4576154b6506e6df1a1dc369b2048.png)
![\frac{1 }{\sqrt[3 ]{2 } } = \frac{1 \cdot \sqrt[3 ]{2 ^{2 } } }{\sqrt[3
]{2 } \cdot \sqrt[3 ]{2 ^{2 } } } = \frac{\sqrt[3 ]{4 } }{\sqrt[3 ]{2 ^{3 } }
} = \frac{\sqrt[3 ]{4 } }{2 }](_images/math/cfdb49e5dcc7c025f6f3b501049fd5eff45023fa.png)
![\frac{ab }{\sqrt[4 ]{x a ^{2 } b ^{3 } } }](_images/math/c7c2f494143e416fb597a9e49d28ef1c0815e6e8.png) il fattore razionalizzante è
il fattore razionalizzante è
![\sqrt[4 ]{x ^{3 } a ^{2 } b }](_images/math/3ca84993ceec50b2ef32593b77d94736a7f19fa6.png)
![\frac{ab }{\sqrt[4 ]{x a ^{2 } b ^{3 } } } = \frac{ab \cdot \sqrt[4 ]{x
^{3 } a ^{2 } b } }{\sqrt[4 ]{x a ^{2 } b ^{3 } } \cdot \sqrt[4 ]{x ^{3 } a
^{2 } b } } = \frac{ab \sqrt[4 ]{x ^{3 } a ^{2 } b } }{\sqrt[4 ]{x ^{4 } a ^{4
} b ^{4 } } } = \frac{ab \sqrt[4 ]{x ^{3 } a ^{2 } b } }{xab } = \frac{\sqrt[4
]{x ^{3 } a ^{2 } b } }{x }](_images/math/642af0ecaf7ffb9744dd314e621b16294269e4c3.png)
![\frac{1 }{\sqrt[3 ]{b ^{5 } } } = \frac{1 }{b \sqrt[3 ]{b ^{2 } } } =
\frac{1 \cdot \sqrt[3 ]{b } }{b \sqrt[3 ]{b ^{2 } } \cdot \sqrt[3 ]{b } } =
\frac{\sqrt[3 ]{b } }{b ^{2 } }](_images/math/ef9815a1c4369ba95d133ba914df72ba5d6b4896.png) con
con
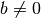 .
.
III Caso
La frazione è del tipo
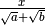 oppure
oppure
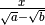
Per questo tipo di frazione occorre sfruttare il prodotto notevole
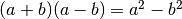 . Il fattore razionalizzante del primo tipo è
. Il fattore razionalizzante del primo tipo è
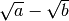 , nel secondo è
, nel secondo è
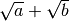 .
.
Sviluppiamo solo il primo tipo, poiché il secondo è del tutto analogo:
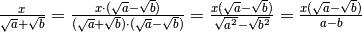
Esempi
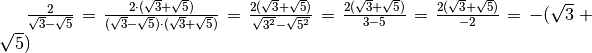
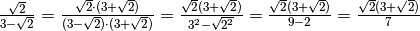
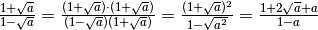 con
con
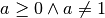
IV Caso
La frazione è del tipo
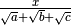
Anche in questo caso si utilizza il prodotto notevole della differenza di quadrati, solo che va ripetuto più volte.
Esempio
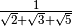 il fattore di razionalizzazione è
il fattore di razionalizzazione è
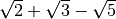
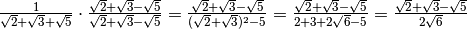 il fattore razionalizzante di questa frazione è
il fattore razionalizzante di questa frazione è
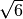 .
.
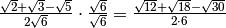 portando fuori radice si ha
portando fuori radice si ha
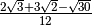
V Caso
La frazione è del tipo
![\frac{x }{\sqrt[3 ]{a } + \sqrt[3 ]{b } }](_images/math/6017afeee305058dbce29d370d084bb0cf23b7d1.png)
Si utilizza il prodotto notevole
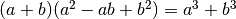 e quello analogo
e quello analogo
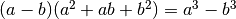
![\frac{x }{\sqrt[3 ]{a } + \sqrt[3 ]{b } } = \frac{x }{\sqrt[3 ]{a } +
\sqrt[3 ]{b } } \cdot \frac{\sqrt[3 ]{a ^{2 } } - \sqrt[3 ]{ab } + \sqrt[3 ]{b
^{2 } } }{\sqrt[3 ]{a ^{2 } } - \sqrt[3 ]{ab } + \sqrt[3 ]{b ^{2 } } } = \frac{x
\left( \sqrt[3 ]{a ^{2 } } - \sqrt[3 ]{ab } + \sqrt[3 ]{b ^{2 } } \right) }{(
\sqrt[3 ]{a } ) ^{3 } + ( \sqrt[3 ]{b } ) ^{3 } } = \frac{x \left( \sqrt[3 ]{a
^{2 } } - \sqrt[3 ]{ab } + \sqrt[3 ]{b ^{2 } } \right) }{a + b }](_images/math/83e217cc58e3f7cc6f71f67fa464c75fd88d4277.png)
Esempio
![\frac{1 }{\sqrt[3 ]{2 } - \sqrt[3 ]{3 } }](_images/math/fe8a4791ffc36eb98adf4cfa61f2b6edbe7759d8.png) il fattore di razionalizzazione è
il fattore di razionalizzazione è
![\sqrt[3 ]{2 ^{2 } } + \sqrt[3 ]{2 \cdot 3 } + \sqrt[3 ]{3 ^{2 } }](_images/math/2991611bf7f77a3474b7d2cbc11b5774ed6bf041.png) quindi
quindi
![\frac{1 \cdot \left( \sqrt[3 ]{2 ^{2 } } + \sqrt[3 ]{2 \cdot 3 } +
\sqrt[3 ]{3 ^{2 } } \right) }{\left( \sqrt[3 ]{2 } - \sqrt[3 ]{3 } \right)
\cdot \left( \sqrt[3 ]{2 ^{2 } } + \sqrt[3 ]{2 \cdot 3 } + \sqrt[3 ]{3 ^{2 } }
\right) } = \frac{\sqrt[3 ]{2 ^{2 } } + \sqrt[3 ]{2 \cdot 3 } + \sqrt[3 ]{3
^{2 } } }{2 - 3 } = - \left( \sqrt[3 ]{4 } + \sqrt[3 ]{6 } + \sqrt[3 ]{9 }
\right)](_images/math/e9e9adac34a11c9895ee68b3a7d5629bccdc3846.png)
Radicali doppi¶
Si dice radicale doppio un’espressione del tipo
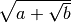 oppure
oppure
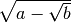
I radicali doppi possono essere trasformati nella somma algebrica di due
radicali semplici se l’espressione
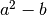 è un quadrato perfetto, la formula per ottenere la trasformazione in radicali
semplici è:
è un quadrato perfetto, la formula per ottenere la trasformazione in radicali
semplici è:
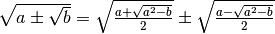
Esempi
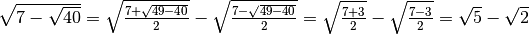 .
.
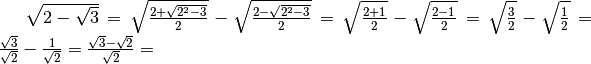
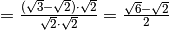 .
.
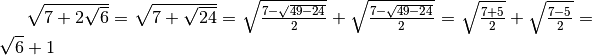 .
.
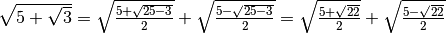 la formula non è stata di alcuna utilità in quanto il radicale doppio non è
stato eliminato.
la formula non è stata di alcuna utilità in quanto il radicale doppio non è
stato eliminato.
Equazioni, disequazioni e sistemi a coefficienti irrazionali¶
Avendo imparato come operare con i radicali puoi risolvere equazioni, sistemi e disequazioni con coefficienti irrazionali.
Disequazioni di primo grado¶
Esempio
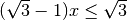 il coefficiente è positivo quindi:
il coefficiente è positivo quindi:
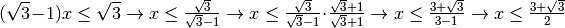
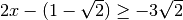 il coefficiente dell’incognita è positivo, quindi
il coefficiente dell’incognita è positivo, quindi
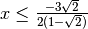 e poi razionalizzando
e poi razionalizzando
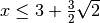
Sistemi di primo grado¶
Esempio
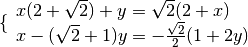 eseguiamo i calcoli per ottenere la forma canonica
eseguiamo i calcoli per ottenere la forma canonica
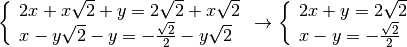 con il metodo di riduzione, sommando le due equazioni otteniamo
con il metodo di riduzione, sommando le due equazioni otteniamo
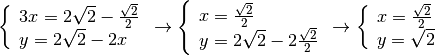
Esercizi¶
Radici¶
- Senza usare la calcolatrice determina per ciascuna delle seguenti radici
quadrate il valore approssimato a 1/10:
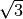 ;
;
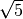 ;
;
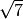 ;
;
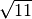 ;
;
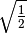 ;
;
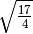
- Estrai le seguenti radici di espressioni letterali, facendo attenzione al
valore assoluto:
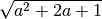 ,
,
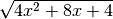 ,
,
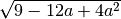
- Determina le seguenti radici quadrate razionali (quando è possibile calcolarle)
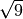 ,
,
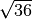 ,
,
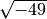 ,
,
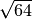 ,
,
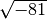
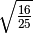 ,
,
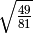 ,
,
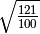 ,
,
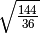 ,
,
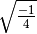
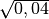 ,
,
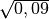 ,
,
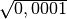 ,
,
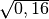 ,
,
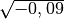
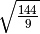 ,
,
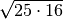 ,
,
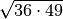 ,
,
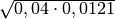 ,
,
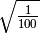
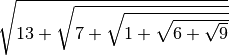 ,
,
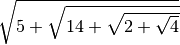
- Senza usare la calcolatrice determina per ciascuna delle seguenti radici
cubiche il valore approssimato a 1/10:
![\sqrt[3 ]{3 }](_images/math/3f8cbe479f775a428b6108dc172c5222c08fb027.png) ,
,
![\sqrt[3 ]{4 }](_images/math/65883b792d0b393260f310e08de3528503ee5a8c.png) ,
,
![\sqrt[3 ]{7 }](_images/math/a3dc9165d5700eff9cd7cf5c18682404ec83db91.png) ,
,
![\sqrt[3 ]{100 }](_images/math/bd758093aa14b93aa5eb4ac1ff8c7623090ffdec.png) ,
,
![\sqrt[3 ]{25 }](_images/math/30e4cdb3ca86d19904df5aeaff9dc2658a0f1c6e.png) ,
,
![\sqrt[3 ]{250 }](_images/math/a952270a66ec2d4e64c91d977cf2373ce87a7634.png)
- Determina le seguenti radici se esistono
![\sqrt[3 ]{27 }](_images/math/e00a3e83c55ed9a354c41ed5fbb5c58e2ca93975.png) ,
,
![\sqrt[3 ]{64 }](_images/math/32c0abb06ad229d22df814a71f9119455e8bf354.png) R.
R.
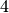 ,
,
![\sqrt[3 ]{- 1 }](_images/math/8ae144707a81c314a3f818cd0deb7350883d22a8.png)
![\sqrt[3 ]{1000 }](_images/math/f96f4a0f323907c3825ffa6a7ce604adbe480764.png) ,
,
![\sqrt[3 ]{125 }](_images/math/fb2e487a52805ca7ff5f61cf59f8c8667019e288.png) ,
,
![\sqrt[3 ]{- 216 }](_images/math/0fb381f7c3fad27c64e0ca8acda4ababd7eb2590.png)
![\sqrt[3 ]{\frac{8 }{27 } }](_images/math/b6cf599d7d3a21dfc671760f2f628375db60d533.png) ,
,
![\sqrt[3 ]{- \frac{64 }{125 } }](_images/math/c03a60f613f440e6db91ad96968f4ed850e6be81.png) ,
,
![\sqrt[3 ]{\frac{1000 }{27 } }](_images/math/35221e214d9074b1da596abf0a5b946481fdfe0b.png) R.
R.
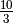
![\sqrt[3 ]{0,001 }](_images/math/e1e0871cce08c688d0888c5034d5f6cdeaa83313.png) ,
,
![\sqrt[3 ]{\frac{1 }{8 } }](_images/math/88b255d30db14989b00566ce701c716f5c64db8e.png) ,
,
![\sqrt[3 ]{- 0,008 }](_images/math/eff259f48613c0364649bb6a94cea5cab3c25ab8.png)
![\sqrt[3 ]{4 + \sqrt[3 ]{61 + \sqrt[3 ]{25 + \sqrt[3 ]{8 } } } }](_images/math/a8d25b11b945dc36c17158e20da35791fc6bbd69.png) ,
,
![\sqrt[3 ]{25 + \sqrt[3 ]{3 + \sqrt[3 ]{122 + \sqrt[3 ]{27 } } } }](_images/math/51eeabebd131d8ae8e28f6fa595fa87e8d38036b.png) R.
R.
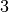 ,
,
![\sqrt[3 ]{27 \cdot \sqrt{64 } }](_images/math/af1d4f688a181596d41769649fd2a533b4b9658e.png)
![\sqrt[9 ]{0 }](_images/math/7f130e7d6e1cf543bf02ab755796a9b44266485d.png)
![\sqrt[8 ]{- 1 }](_images/math/ce90151c4ed9c586b989082a71bc0a632b8f41ce.png) R. non esiste,
R. non esiste,
![\sqrt[5 ]{- 100000 }](_images/math/02b5bda362ac6458e38a5c7b876bb0ffd4fdbca1.png)
![\sqrt[4 ]{0,0001 }](_images/math/92330799870eeb337612a7c4025a9175ca0de490.png) ,
,
![\sqrt[4 ]{81 }](_images/math/54102310c7d82be85bcf5009c5b8102234223290.png) ,
,
![\sqrt[6 ]{64 }](_images/math/7105dd262da6cc54ced833f3cdcf927f6da80146.png)
![\sqrt[5 ]{\frac{32 }{243 } }](_images/math/27bdc84fc5b3b392e4065334d207f439ff55dc08.png) R.
R.
 ,
,
![\sqrt[4 ]{- 4 }](_images/math/4bc33479b65a25c1fff4d7adb8bf1af4d491ce31.png) ,
,
![\sqrt[10 ]{0 }](_images/math/e68b2a8ed32cee1d34fc78055c3ec154a2fe2716.png)
![\sqrt[4 ]{0,0081 }](_images/math/cb1e0e6a1fcaa73d5bbbfc990c60b6a9e046ba76.png) ,
,
![\sqrt[5 ]{34 - \sqrt[4 ]{14 + \sqrt{2 + \sqrt[3 ]{8 } } } }](_images/math/51da9714dcad89202c4ff3f6b0ff2c0f447733c6.png) R.2,
R.2,
![\sqrt{20 + \sqrt[3 ]{121 + \sqrt[4 ]{253 + \sqrt[5 ]{243 } } } }](_images/math/948267ba639beccd0875fe7eb247215d7d333732.png)
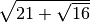 ,
,
![\sqrt[5 ]{31 + \sqrt[4 ]{1 } }](_images/math/f8e3b59fad0c7bcf99982f67cc1158cabf6428fd.png) ,
,
![\sqrt[5 ]{240 + \sqrt{9 } }](_images/math/b93e1beead31fd305d4a634569c3f357a75b21de.png) R.3
R.3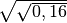 ,
,
![\sqrt[5 ]{32 \cdot 10 ^{- 5 } }](_images/math/5645dee73e685f04d6b2d4c0b44effd34afefbb7.png) R.0,2,
R.0,2,
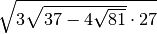 R.5
R.5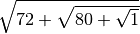 ,
,
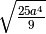 ,
,
![\sqrt[4 ]{620 + \sqrt[4 ]{625 } }](_images/math/4c8e1c2bc11a19ff8b0a0a066176f67254c44e86.png)
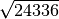
![\sqrt[5 ]{243 }](_images/math/5ac56d6a242b114251f37d61ad7bc54b30c9bb18.png)
![\sqrt[4 ]{600 + \sqrt{25 } \cdot \sqrt{25 } }](_images/math/c390a84da46c63119cbfa2d4890634fd4e5148b7.png)
![\sqrt[3 ]{8a ^{3 } + 12a ^{2 } + 6a + 1 }](_images/math/736847cbed0fefa44a73087ed8acc88b4b30acec.png) R.(2a+1),
R.(2a+1),
![\sqrt[3 ]{a ^{6 } + 9a ^{4 } + 27a ^{2 } + 27 }](_images/math/564206f6b2aef12da915b381037fd4592df8d290.png) R.
R.
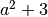 ,
,
![\sqrt[3 ]{1 - 6x + 12x ^{2 } - 8x ^{3 } }](_images/math/c3e089c68983deae85b3f5557bc0c162897e7cbf.png) R.1-2x
R.1-2x
Condizioni di esistenza¶
Determina le condizioni di esistenza dei seguenti radicali.
![\sqrt[3 ]{x + 1 }](_images/math/37e079d79b977ac41fc6aba73b02b8e4f135027b.png) R.
R.
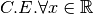 ,
,
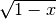 R.
R.
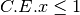
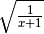 R.
R.
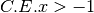 ,
,
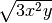 R.
R.
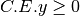
![\sqrt[3 ]{3xy }](_images/math/744068dad7ea2fc992a2c27f027d6f0c5e1bec2c.png)
![\sqrt[4 ]{- 2x ^{2 } y ^{2 } }](_images/math/7ba09521d342b1d8e39a4c1a7577719446607e2e.png)
![\sqrt[4 ]{\frac{x ^{2 } + 1 }{x - 1 } }](_images/math/39133a5f45efc9dca63373c6c97b99d7f9d077df.png) R.
R.
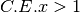 ,
,
![\sqrt[5 ]{\frac{1 }{x ^{3 } } }](_images/math/03031f01fed5c0ed76d912128f0727cebbf68e84.png)
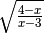 ,
,
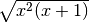 R.
R.
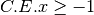
![\sqrt[3 ]{1 + a ^{2 } }](_images/math/16d98bdba7071c652c9ff922e3d1a3312efd618e.png) .
.
![\sqrt[6 ]{2x - 1 }](_images/math/58d72ba6be9df4e08ecbd008837eb7eab0231078.png)
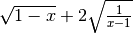 R. nessun valore,
R. nessun valore,
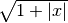
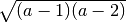 ,
,
![\sqrt{\left\lvert x \right\rvert + 1 } \cdot \sqrt[3 ]{x + 1 }](_images/math/e412c23bd8034be91584d0acc3587156b061403e.png)
![\sqrt[3 ]{\frac{x ^{2 } + x + 1 }{x ^{2 } + 2x + 1 } }](_images/math/b885aedcc8b6e6bfcb6c3c25acaae20573ad7137.png) ,
,
![\sqrt{\frac{1 }{x ^{2 } } - 1 } \cdot \sqrt[4 ]{\frac{x - 1 }{3 - x }
}](_images/math/52db60c1e5599fff7a6ac8050ecec5b256dc1af3.png) R.
R.
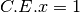
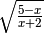 R.
R.
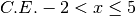 ,
,
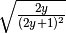
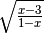 ,
,
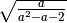
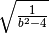 R.
R.
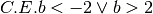 ,
,
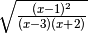
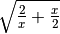 ,
,
![\sqrt[6 ]{\frac{x - 1 }{\left\lvert x \right\rvert } }](_images/math/3cd78f017ca6e05a9b9aea5e310004760692a664.png)
![\sqrt[4 ]{\frac{4 x ^{2 } + 4 + 8 x }{9 } }](_images/math/bc35fe71e33346714fd4345ef8b5e4a9161b0410.png) ,
,
![\sqrt[6 ]{\frac{\left( b ^{2 } + 1 + 2 b \right) ^{3 } }{729 b ^{6 }
} }](_images/math/f8453ef410f2f47575cde3797982482dffec0ec3.png)
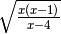 R.
R.
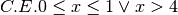 ,
,
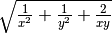
![\sqrt[4 ]{\frac{m + 1 }{m - 1 } }](_images/math/b1d39cea643ad74d794253365dea37aef69679f0.png) ,
,
![\sqrt[3 ]{x ( x + 2 ) ^{2 } }](_images/math/680f28270dc98bc5a57b893048c3ea832671e9ed.png)
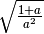 ,
,
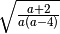 R.
R.
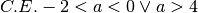
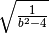 ,
,
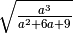
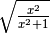 R.
R.
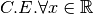 ,
,
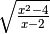
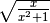 ,
,
![\sqrt[3 ]{\frac{x ^{3 } }{x ^{3 } + 1 } }](_images/math/66f9fd201233a9948d84f21532ee4ecba86a7cfd.png) R.
R.
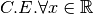
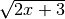 ,
,
![\sqrt[3 ]{a ^{2 } - 1 }](_images/math/61d5852d81536abc9d5f8d8cff0cbd6652167540.png)
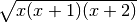 R.
R.
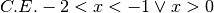 ,
,
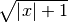 R.
R.
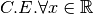
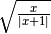 R.
R.
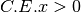 ,
,
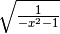 R. nessun valore
R. nessun valore
Potenze a esponente razionale¶
Calcola le seguenti potenze con esponente razionale
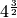 ,
,
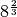 ,
,
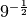 ,
,
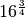
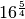 ,
,
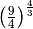 ,
,
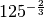 R.
R.
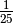 ,
,
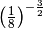
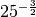 ,
,
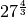 ,
,
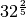 R.4,
R.4,
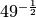
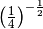 ,
,
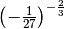 ,
,
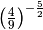 ,
,
 R.25
R.25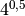 ,
,
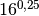 ,
,
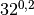 R.2,
R.2,
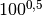
- Trasforma le seguenti espressioni in forma di potenza con esponente frazionario
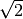 ,
,
![\sqrt[3 ]{8 ^{2 } }](_images/math/43e621fdb0d06e96e9410b386a5aafb80314a28c.png) ,
,
![\sqrt[7 ]{5 ^{3 } }](_images/math/c78ba78495d76b5b421cb80db41fffa890da47e1.png) R.
R.
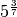 ,
,
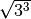
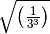 ,
,
![\sqrt[3 ]{\frac{1 }{3 ^{2 } } }](_images/math/f83b3ecdcb98f5ae81b53b34e1f3fae49b6cf018.png) ,
,
![\sqrt[3 ]{\frac{1 }{25 } }](_images/math/932d6b706403d51ca1eb607d5072524c2359841f.png) R.
R.
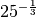 ,
,
![\sqrt[5 ]{\frac{4 ^{2 } }{3 ^{2 } } }](_images/math/55a48711edc51923436b2eac3a4e1a6fae2e2a5d.png)
- Trasforma nella forma radicale:
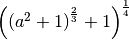 R.
R.
![\sqrt[4 ]{\sqrt[3 ]{( a ^{2 } + 1 ) ^{2 } + 1 } }](_images/math/6dce48d7f4f131376054c57dac43e5076ef2a99a.png) ,
,
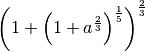
- Scrivi in ordine crescente i seguenti numeri:
 ,
,
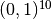 ,
,
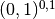 ,
,
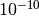 ,
,

Semplificazione delle radici¶
Trasforma i seguenti radicali applicando la proprietà invariantiva
![\sqrt[4 ]{4 } = \sqrt[8 ]{\dots }](_images/math/b4fcf1769a7d0852a95ec83fda825c3172326fa4.png)
![\sqrt[3 ]{9 } = \sqrt[6 ]{\dots }](_images/math/8b39ccf264e337c0858c81e2e7fbf2f8c7aa1f91.png)
![\sqrt[5 ]{5 } = \sqrt[15 ]{\dots }](_images/math/1b764eb08e1ba9d0e68c07a0eac77ee243a37ba5.png)
![\sqrt{2 } = \sqrt[6 ]{\dots }](_images/math/c41127426058f369f86d672cbf1803a0978b1d2d.png)
![\sqrt{2 } = \sqrt[\dots ]{16 }](_images/math/a952702f1ec2786647e153107cf9fa49f67c3f45.png)
![\sqrt[3 ]{3 } = \sqrt[\dots ]{81 }](_images/math/af5f81b027d916597381fd33781b8a25a19f7fbd.png)
![\sqrt[3 ]{- 5 } = - \sqrt[\dots ]{25 }](_images/math/6d4a03f3502b6633109cdd6f53819af75b65a0ea.png)
![\sqrt[4 ]{\frac{3 }{2 } } = \sqrt[\dots ]{\frac{27 }{8 } }](_images/math/30f6ba1c3792b51458ef2801cb53a78c8a377e02.png)
![\sqrt[21 ]{a ^{7 } } = \sqrt[6 ]{\dots }](_images/math/28336be1cf460b062449da6a461ba823c0d4dff3.png) con a>0
con a>0
![\sqrt[8 ]{a ^{24 } } = \sqrt[5 ]{\dots }](_images/math/4af4cc49d1accf83c4fd0f62ab0eba8868cc6e0f.png) con a>0
con a>0
![\sqrt[3 ]{27 } = \frac{1 }{\sqrt{\dots } }](_images/math/27c93ae0ccf65c5c4aab5e71a9961c8032e6d6d8.png)
![\sqrt{x ^{4 } + 2x ^{2 } + 1 } = \sqrt[7 ]{\dots }](_images/math/3ffed8bda893e87d4da3b5f5a1c6be284101020d.png)
Semplifica i radicali
![\sqrt[4 ]{25 }](_images/math/edbb9d9d61c8208b8c56032730add54037553859.png) ,
,
![\sqrt[6 ]{8 }](_images/math/dc903bda47a96b9f0ff1d8642917cec192b52351.png) ,
,
![\sqrt[8 ]{16 }](_images/math/b537d524aa300717f90b038fbefc26e62a980635.png) R.
R.
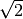
![\sqrt[9 ]{27 }](_images/math/351ff20241f89928a1cc4d1d993f2a7238cc7b9c.png) ,
,
![\sqrt[4 ]{100 }](_images/math/15356eb7a081c25ba467e60e31dca628c70f266e.png) R.
R.
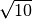 ,
,
![\sqrt[6 ]{144 }](_images/math/893b0310edba57ce52743563990d311134910311.png)
![\sqrt[4 ]{169 }](_images/math/03ae91823fb3a598715ea52d4393bec2b206b13d.png) ,
,
![\sqrt[6 ]{121 }](_images/math/1999f34d1adbab0de70e6642397a32ac19aeb77d.png) ,
,
![\sqrt[6 ]{125 }](_images/math/a61c986cc92629a7bf6bc79d45c8f16808d5e9d6.png) R.
R.
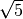
![\sqrt[4 ]{49 }](_images/math/dab52c0e2ea3a73880c416bd0cf6527e913b6206.png) ,
,
![\sqrt[6 ]{64 }](_images/math/7105dd262da6cc54ced833f3cdcf927f6da80146.png) R. 2,
R. 2,
![\sqrt[12 ]{16 }](_images/math/461d42fbe2fe6310feac90a10f3a6ec1d0e9c062.png)
![\sqrt[6 ]{\frac{16 }{121 } }](_images/math/1faa1d9dd722637207e53384039fbbbbf634cf71.png) R.
R.
![\sqrt[3 ]{\frac{4 }{11 } }](_images/math/4db5764e5619e1e8ee1775f52875626691a62e8d.png) ,
,
![\sqrt[4 ]{\frac{1 }{16 } }](_images/math/b37abfb1c1908fa4a8ff49e23d986a46d43b718a.png) ,
,
![\sqrt[10 ]{\frac{25 }{81 } }](_images/math/aa6eaa308778e22beca2b2076f13e6d3d57c191f.png)
![\sqrt[15 ]{\frac{64 }{27 } }](_images/math/f5a61a0929a7cfd59b3a5e21e9ecf5c12777f5e4.png) ,
,
![\sqrt[9 ]{- 3 ^{3 } }](_images/math/515748aa5add5ea582e0fd0b46d5e62160cef0e1.png) R.
R.
![\sqrt[3 ]{- 3 }](_images/math/570c8c45e7772db57bbc4bf04c8191478770f022.png) ,
,
![\sqrt[6 ]{( - 2 ) ^{4 } }](_images/math/b4ee8ed4bf40d59e37def3a5b5d954a70e34cce1.png)
![\sqrt[12 ]{- 4 ^{6 } }](_images/math/c80864bbe1f48d07475b90cc05390b3941ae8aae.png) R. impossibile,
R. impossibile,
![\sqrt[10 ]{- 32 }](_images/math/6fa6d51b76e6990cb481e9bbb4c932d5e5c06576.png) ,
,
![\sqrt[6 ]{5 ^{2 } - 4 ^{2 } }](_images/math/f3da61cd31ef82bfe2e7edfd0caa6a3973643c1c.png)
![\sqrt[4 ]{12 ^{2 } + 5 ^{2 } }](_images/math/8d55aaa2347887a52eb80bbe550eb76eab740504.png) ,
,
![\sqrt[10 ]{3 ^{2 } + 4 ^{2 } }](_images/math/47187636761392fc203e8239dcedc68d85519d71.png) R.
R.
![\sqrt[5 ]{5 }](_images/math/e468301379750729c47fb4de106bc2c5f5beb878.png) ,
,
![\sqrt[4 ]{10 ^{2 } - 8 ^{2 } }](_images/math/f7c7db6485a57137291ba62240b195a3150c8b80.png)
![\sqrt[3 ]{2 ^{6 } \cdot 5 ^{15 } }](_images/math/57318b6d133ec8d3e1551cb37e3b52d15c787352.png) R. 12.500,
R. 12.500,
![\sqrt[4 ]{3 ^{4 } \cdot 4 ^{6 } }](_images/math/c589a32f2fa815c9667a29fc75c87983f0d79c45.png) ,
,
![\sqrt[5 ]{5 ^{5 } \cdot 4 ^{10 } \cdot 2 ^{15 } }](_images/math/eadc1ec25f85d2882a419b271d204537a1db3e69.png)
![\sqrt[9 ]{27 \cdot 8 \cdot 125 }](_images/math/58c29b289cff9120792be8d3f0eb55fa53d690d6.png) ,
,
![\sqrt[4 ]{625 }](_images/math/242cfb4814ebf9de02b8af55cee7aaa6c0cc9c7e.png) R. 5,
R. 5,
![\sqrt[6 ]{1000 }](_images/math/b08676d8cd995cdfecb8c7e0024c096197144d85.png)
![\sqrt[4 ]{2 + \frac{17 }{16 } }](_images/math/62c0d5d8554d8afbe4d27991dc27bc4004a224e5.png) ,
,
![\sqrt[6 ]{\left( \frac{13 }{4 } + \frac{1 }{8 } \right) ^{4 } }](_images/math/91e17e9acd951eff45638708f71d18c0ed238390.png) R.
R.
 ,
,
![\sqrt[6 ]{\left( 1 + \frac{21 }{4 } \right) ^{3 } }](_images/math/e171990cad7c0cbbedb9d804589ce965df40abb5.png)
![\sqrt[16 ]{( - 16 ) ^{4 } }](_images/math/4dd63f43bfcf22af3ce19536ddc88a1f7a4804bc.png) R. 2,
R. 2,
![\sqrt[10 ]{2 ^{10 } \cdot 3 ^{20 } }](_images/math/b01afbb918c65f7397b1cfa222dc8f6307c074c3.png) ,
,
![\sqrt[6 ]{2 ^{8 } \cdot 3 ^{6 } }](_images/math/c88b8fd61ebeeecf8dc9dfa6279192caf69bc7ee.png)
![\sqrt[12 ]{3 ^{6 } \cdot 4 ^{12 } }](_images/math/171b4ba9ef4dd0d7800d246379f956802139d8ee.png) R.
R.
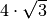 ,
,
![\sqrt[4 ]{2 ^{10 } \cdot 3 ^{15 } \cdot 12 ^{5 } }](_images/math/99ae8c05f4d89006d13fd7fd9eb9161b1afc72be.png) ,
,
![\sqrt[6 ]{3 ^{9 } \cdot 8 ^{2 } }](_images/math/f65eee4f38b2c8e60dda7fab4d8a964c9a473f99.png)
![\sqrt[4 ]{9x ^{2 } y ^{4 } }](_images/math/c432c6f37b97ced8699d99745191bffb188d5769.png) ,
,
![\sqrt[3 ]{64a ^{6 } b ^{9 } }](_images/math/491c91fa33e8f11d17c65d3d025d079e42372525.png) R.
R.
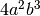 ,
,
![\sqrt[3 ]{x ^{6 } y ^{9 } ( x - y ) ^{12 } }](_images/math/e5a8a4cfbdc3e85d97ffe5349d0b655194cb1e25.png)
![\sqrt[5 ]{\frac{32a ^{10 } }{b ^{20 } } }](_images/math/373486c594add0f26f481c5853507cec037afa56.png) ,
,
![\sqrt[4 ]{\frac{20a ^{6 } }{125b ^{10 } } }](_images/math/5a6a4ffd5749a90228af41fe93f304892575eaee.png) ,
,
![\sqrt[8 ]{\frac{16 x ^{5 } y ^{8 } }{81 x } }](_images/math/8014fec39643e818f43c299454796c5b00510017.png) R.
R.
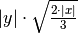
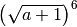 ,
,
![\sqrt[9 ]{27 a ^{6 } b ^{12 } }](_images/math/1f0ea1246e31dcf2b81c62557d651271fc7e14dd.png) ,
,
![\sqrt[12 ]{( 2 x + 3 ) ^{3 } }](_images/math/f2c8241611850324efaced813c028ece6674c7d9.png) R.
R.
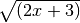
![\sqrt[6 ]{\frac{0,008 x ^{15 } y ^{9 } }{8 a ^{18 } } }](_images/math/1f400b5048dce95f7dc3d838d433bcf0369fca70.png)
![\sqrt[10 ]{\frac{121 a ^{5 } }{a b ^{2 } } }](_images/math/d934e7149be988a45bdd186ffb4a361d80585500.png) R.
R.
![\sqrt[5 ]{\frac{11 a ^{2 } }{b } }](_images/math/15770a08af3464a428bbc3aee6c29dfab13c3a9f.png)
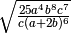
![\sqrt[6 ]{a ^{2 } + 2 a + 1 }](_images/math/f9209489dea0174f87b309284179fcb82f29fd5a.png) ,
,
![\sqrt[9 ]{a ^{3 } + 3 a ^{2 } + 3 a + 1 }](_images/math/ec88870ba0b55134c9d810127546b11c6db69d04.png) ,
,
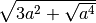 R.
R.
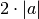
![\sqrt[4 ]{x ^{4 } + 2 x ^{2 } + 1 }](_images/math/7c87c39a9034e59fcd1ddf0ce2ce160d5a3b8247.png) ,
,
![\sqrt[10 ]{a ^{4 } + 6 a ^{2 } x + 9 x ^{2 } }](_images/math/3dca2003a4084ad431c29035833824bf453a269b.png) R.
R.
![\sqrt[5 ]{\left\lvert a ^{2 } + 3 x \right\rvert }](_images/math/ab8bb98a0bdc2a67847210b1c53c3c31877ae093.png) ,
,
![\sqrt[6 ]{8 a ^{3 } - 24 a ^{2 } + 24 a - 8 }](_images/math/20229d5fba962b7ef9d0d928af0ea6adea37bdb5.png)
![\sqrt[6 ]{\frac{9 x ^{2 } }{y ^{6 } } }](_images/math/1fabf4fe95cadfe503907b2f350e74e2e612b5a9.png) ,
,
![\sqrt[4 ]{\frac{16 a ^{4 } b ^{6 } }{25 x ^{2 } } }](_images/math/36f1d4097ba269baa2efcb6154e23dc9d5b8a98f.png) ,
,
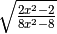 R.
R.

![\sqrt[8 ]{a ^{4 } + 2 a ^{2 } x ^{2 } + x ^{4 } }](_images/math/ae8fff24d35c5307a6a66763f1aa1a1602fb3068.png) ,
,
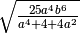 R.
R.
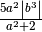 ,
,
![\sqrt[9 ]{x ^{6 } + 3 x ^{5 } + 3 x ^{4 } + x ^{3 } }](_images/math/8e7c0ed59cd4f62adda791f05e134356ab796a45.png)
![\sqrt[4 ]{a ^{2 } + 6 a + 9 }](_images/math/d983b4cde4bd6554ce8f254732cc8a0817f48a2d.png) ,
,
![\sqrt[9 ]{8 x ^{3 } - 12 x ^{2 } + 6 x + x ^{3 } }](_images/math/60c9c6acacf3cb427197c154fe9f954b1f8dd7c1.png) ,
,
![\sqrt[4 ]{a ^{4 } ( a ^{2 } - 2 a + 1 ) }](_images/math/0608ebf29b2f0756aa6bd23f249aeee38ea3190f.png) R.
R.
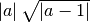
![\sqrt[4 ]{( x ^{2 } - 6 x + 9 ) ^{2 } }](_images/math/954c18e2fd5d3661591917cb66488972edb02e05.png) R.
R.
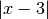 ,
,
![\sqrt[12 ]{( x ^{2 } + 6 x + 9 ) ^{3 } }](_images/math/b203210d272de4ec39e8cfe81da33fee84967f6c.png) ,
,
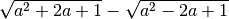
![\sqrt[18 ]{\frac{a ^{9 } + 3 a ^{8 } + 3 a ^{7 } + a ^{6 } }{9 a ^{7 }
+ 9a ^{5 } + 18 a ^{6 } } }](_images/math/d184d5a9d6eacf22c69e076d4b2d59c7637fbe94.png) ,
,
![\sqrt[6 ]{\frac{( x ^{2 } + 1 - 2 x ) ^{3 } b }{b ^{7 } \left( x ^{3 }
+ 3 x ^{2 } + 3 x + 1 \right) ^{2 } } }](_images/math/6e895bc8a2b3028be14ea278021bb9e5656770a3.png) R.
R.
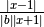 ,
,
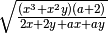
![\sqrt[2 n ]{16 ^{n } }](_images/math/3f655ee61a379ff6f7d35ee8fde58baee681e692.png) ,
,
![\sqrt[4 n ]{\frac{2 ^{3 n } }{3 ^{2 n } } }](_images/math/cfbd9371f3fde60e319aceb2bae1944b62a4d7b9.png) R.
R.
![\sqrt[4 ]{\frac{8 }{9 } }](_images/math/aa64f3d97e84ed84c410eff4573654c1cea5d2c0.png) ,
,
![\sqrt[n ^{2 } ]{\frac{6 ^{2 n } }{5 ^{3 n } } }](_images/math/928d0ec5c3f402d2be91df8c01bbd50aad16ae2d.png)
![\sqrt[3 n ]{27 ^{n } \cdot 64 ^{2n } }](_images/math/97fb79cc8fbd9959bcc10e7a374fc2be7be8cf72.png) ,
,
![\sqrt[2n ^{2 } ]{16 ^{2n } \cdot 81 ^{2n } }](_images/math/25910d4c499f4db3362f29216e98903bfd606bdb.png) R.
R.
![\sqrt[n ]{6 ^{4 } }](_images/math/dc35ff861c064a9127e1f75fbd6c0bb666e6ee64.png) ,
,
![\sqrt[n + 1 ]{16 ^{2n + 2 } }](_images/math/84bdbc3a612920fb2a7a562742c74db98cce1279.png)
![\sqrt[5 ]{25 x ^{3 } y ^{4 } }](_images/math/bc70d028dce9096661483ec7e0348002632b0b90.png) ,
,
![\sqrt[12 ]{81 a ^{6 } b ^{12 } }](_images/math/eaa4c04dc43001179d640685f6ae755650c5056c.png) ,
,
![\sqrt[5 ]{32 x ^{10 } }](_images/math/9e2ee3b4a73f3bfe8b507d8c881f7e5d2a6f41a8.png) R.
R.
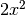
Moltiplicazione e divisione di radici con indici diversi¶
Esegui le seguenti moltiplicazioni e divisioni di radicali (le lettere, dove compaiono, rappresentano numeri reali positivi)
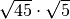 R. 15,
R. 15,
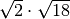 ,
,
![\sqrt[3 ]{16 } \cdot \sqrt[3 ]{4 }](_images/math/89ca45b00f01775924eb565b2156640c1dfc8fb0.png)
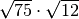 R. 30,
R. 30,
![\sqrt[3 ]{20 } \cdot \sqrt{50 }](_images/math/4c3cef0ac21bd3db2e7106719fa7637542e61f5c.png) ,
,
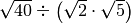
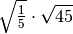 ,
,
![\sqrt[3 ]{3 } \div \sqrt[3 ]{9 }](_images/math/ed48ee4bcb0785dda82d68e7d37fe766f613006e.png) ,
,
![\sqrt[5 ]{2 } \cdot \sqrt[5 ]{6 } \div \sqrt[5 ]{12 }](_images/math/c8e5e49b32ab6b076f8fbd4c484b8f79230719da.png) R. 1
R. 1![\sqrt[6 ]{81 } \cdot \sqrt[6 ]{81 } \div \sqrt[6 ]{9 }](_images/math/6a81b9d9d9ce372bc7fa03e877eca6bdea7c509c.png) ,
,
![\sqrt[4 ]{1 + \frac{1 }{2 } } \cdot \sqrt[4 ]{2 - \frac{1 }{2 } }
\cdot \sqrt[4 ]{1 + \frac{5 }{4 } }](_images/math/cd2e1beddba9004ddaf0d94a5d77be0950bbeac2.png) ,
,
![\sqrt{3 } \cdot \sqrt[3 ]{9 }](_images/math/9f4c266ee3031b319522e683ae8c2035a352ddbe.png) R.
R.
![\sqrt[6 ]{3 ^{7 } }](_images/math/694dcf15cd56609de3a86d55fe442444cf4508e4.png)
![\sqrt[3 ]{2 } \cdot \sqrt{8 }](_images/math/84b8a905030b29fe1769e9142d4ddc1e7d283182.png) ,
,
![\sqrt[6 ]{81 } \cdot \sqrt{3 }](_images/math/03c8ba7b99b5765aa972b1f159c58e68f0dbaf0d.png) R.
R.
![\sqrt[6 ]{3 ^{7 } }](_images/math/694dcf15cd56609de3a86d55fe442444cf4508e4.png) ,
,
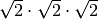
![\sqrt{\frac{10 }{3 } } \cdot \sqrt[3 ]{\frac{6 }{5 } } \div \sqrt[4
]{\frac{2 }{25 } }](_images/math/37213a5244a10faddcb05b55202a92557ab2bd42.png) ,
,
![\sqrt{\frac{10 }{2 } } \cdot \sqrt[3 ]{\frac{6 }{3 } } \div \sqrt[6
]{\frac{4 }{9 } }](_images/math/5e8864bed89bf1d9a141e3a32acb6855bf1bd3e0.png) R.
R.
![\sqrt[6 ]{\frac{3 ^{2 } \cdot 5 ^{3 } }{4 ^{2 } } }](_images/math/7b7566199a28b0ac7b8a48fdf8d2e965a6fcdc2d.png) ,
,
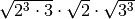
![\left( \sqrt[3 ]{\frac{42 }{13 } } \div \sqrt[3 ]{\frac{91 }{36 }
} \right) \div \sqrt{13 }](_images/math/cb0fd13fb01908e4b5580b6c316ec49eb731440b.png) ,
,
![\sqrt[3 ]{\frac{3 }{4 } } \cdot \sqrt[3 ]{\frac{25 }{24 } }
\cdot \sqrt[3 ]{\frac{5 }{2 } }](_images/math/723c6ab2ae845d3ba494043768fc3694d016f714.png) R.
R.
 ,
,
![\sqrt[3 ]{5 + \frac{1 }{3 } } \cdot \sqrt[3 ]{\frac{4 }{3 } }](_images/math/de6eecc632036d4207849ac16e7d8f8708a5e921.png)
![\sqrt[5 ]{2 ^{3 } } \cdot \sqrt[10 ]{2 ^{4 } }](_images/math/fbfb7263dd8e19a3ea0449ae891deee3519b6437.png) R. 2,
R. 2,
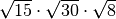 R. 60,
R. 60,
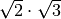
![\sqrt[3 ]{- 1 - \frac{1 }{2 } } \div \sqrt{1 - \frac{1 }{2 } }
\cdot \sqrt[6 ]{12 }](_images/math/557bb204bc5a5299c7dffebf8bc7c4165adec0f0.png) ,
,
![\sqrt[3 ]{1 + \frac{1 }{2 } } \cdot \sqrt[4 ]{2 + \frac{1 }{4 } }](_images/math/508973b871c776b12bd6cf5edc6b6bcb79900f84.png) R.
R.
![\sqrt[6 ]{\frac{3 ^{5 } }{2 ^{5 } } }](_images/math/7f7186a89b3a5887935fcb4cba96b00c438ca4f9.png)
![\sqrt[3 ]{4 a } \cdot \sqrt[3 ]{9 a } \cdot \sqrt[3 ]{12 a }](_images/math/a40bc568907512fd84215a2a120a0444952b0453.png) ,
,
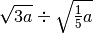 R.
R.
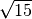
![\sqrt[3 ]{2 ab } \cdot \sqrt[3 ]{4 a ^{2 } b ^{2 } }](_images/math/ffbf46e0f3a6f4383ed3b2a99b160cee49a90e19.png) R. 2ab,
R. 2ab,
![\sqrt{x } \cdot \sqrt[3 ]{x ^{2 } } \div \sqrt[6 ]{x }](_images/math/b6a2b4af66bf8e296ff9539b4a1187e00a34d711.png)
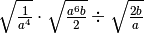 ,
,
![\sqrt{\frac{4 }{9 } } \cdot \sqrt{\frac{3 }{2 } a } \div \sqrt[6 ]{3
a }](_images/math/18a490d4148a8d779ade9fc519b1ea3624a9d0ff.png) R.
R.
![\sqrt[6 ]{\frac{2 ^{3 } a ^{2 } }{3 ^{4 } } }](_images/math/6ddeed0af8a997a249f6ffa8feb17714e2a17d65.png)
![\sqrt[3 ]{a x } \cdot \sqrt{x y } \cdot \sqrt[5 ]{a y }](_images/math/2cfaac143c0215ea742c13697e19ec16eeb67bce.png) ,
,
![\sqrt[3 ]{( x + 1 ) ^{2 } } \div \sqrt{x - 1 }](_images/math/b0f51d996e5f00496a8f83a40bde82e4490f4d1f.png) R.
R.
![\sqrt[6 ]{\frac{( x + 1 ) ^{4 } }{( x - 1 ) ^{3 } } }](_images/math/49213d4590875401297e56b40db93762d429fe43.png)
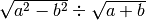 R.
R.
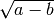 ,
,
![\sqrt{a ^{2 } - 3 a } \cdot \sqrt[3 ]{a ^{2 } } \cdot \sqrt[6
]{a ^{5 } }](_images/math/0f963fc553a7870d5bc82e228a2794d4ddb90260.png)
![\sqrt{\frac{1 - x }{1 + x } } \cdot \sqrt[3 ]{\frac{1 - x ^{2 } }{1 +
x ^{2 } } }](_images/math/6db34da8eccad6910c1b52ef06edd0de57d3c544.png) R.
R.
![\sqrt[6 ]{\frac{( 1 - x ) ^{4 } }{( 1 + x ) ( 1 + x ^{2 } ) ^{2 } } }](_images/math/a8136502c3649c2573393eb28cf85e7db08d03ce.png) ,
,
![\sqrt{\frac{a + b }{a - b } } \div \sqrt[3 ]{\frac{a + b }{a - b } }](_images/math/81b47487f044c756ba3ebe945b2fa427c515ea01.png)
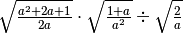 ,
,
![\sqrt{\frac{a + 1 }{a - 3 } } \cdot \sqrt[3 ]{\frac{a ^{2 } - 9 }{a
^{2 } - 1 } }](_images/math/2e00079bf929331e9a35db288203d29aaef5c1b4.png) R.
R.
![\sqrt[6 ]{\frac{( a + 1 ) ( a + 3 ) ^{2 } }{( a - 3 ) ( a - 1 ) ^{2 }
} }](_images/math/c672d2294c43d6ebde24e7d65ab2bd57c77c868e.png)
![\sqrt{\frac{x + 1 }{x - 2 } } \cdot \sqrt{\frac{x - 1 }{x + 3 } } \div
\sqrt[3 ]{\frac{x ^{2 } - 1 }{x ^{2 } + x - 6 } }](_images/math/6fa61afdb56ab2175b03f7ed18469404fe09aa5e.png) R
R
![\sqrt[6 ]{\frac{( x - 1 ) ( x + 1 ) }{( x - 2 ) ( x + 3 ) } }](_images/math/6549a967c6fa9e24396ec0d8c0bfc7829f2808d9.png) ,
,
![\sqrt{a ^{4 } b } \cdot \sqrt[6 ]{\frac{a ^{2 } }{b } }](_images/math/e3a7003463dd1b9864bc826d9e63fca6e06c7cd1.png)
![\sqrt[3 ]{\frac{a ^{2 } - 2 }{a + 3 } } \cdot \sqrt[4 ]{\frac{a + 3
}{a - 2 } }](_images/math/99f302d6cc4705b77453a989690fe12f087fba22.png) ,
,
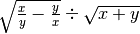 R.
R.
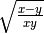
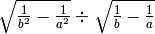 R.
R.
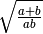 ,
,
![\frac{\sqrt{4 a ^{2 } - 9 } \cdot \sqrt{2 a - 3 } }{\sqrt[3 ]{2 a + 3
} }](_images/math/22e50f7d77d4cd6287ae08b378257e90f21126d2.png)
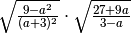 ,
,
![\sqrt{\frac{a + 2 }{a - 1 } } \div \sqrt[3 ]{\frac{( a - 1 ) ^{2 }
}{a ^{2 } + 4 a + 4 } }](_images/math/afa22fbf0cbb30d6c00aee71c23352344e3693f1.png) R.
R.
![\sqrt[6 ]{\frac{( a + 2 ) ^{7 } }{( a - 1 ) ^{7 } } }](_images/math/91df02775f4dd6fa0714f364c7a9ffdf1cbc8cfd.png)
![\sqrt{\frac{x ^{2 } - 4 }{x + 1 } } \cdot \sqrt[3 ]{\frac{1 }{x ^{3 }
- 2 x ^{2 } } }](_images/math/25a1a6db87fdbee5a70f9186043df9bc76af9357.png) R.
R.
![\sqrt[6 ]{\frac{x + 2 }{x ^{2 } ( x + 1 ) } }](_images/math/3f868477ed61bc1700389c67a6602785158c2112.png) ,
,
![\sqrt[4 ]{\frac{a + b }{a ^{2 } - b ^{2 } } } \cdot \sqrt[3 ]{\frac{a
- 2 b }{a + 2 b } } \cdot \sqrt[6 ]{a ^{2 } - 4 b ^{2 } }](_images/math/d8a9a40e19b4cf564bf2cef0ae072ef6ee60d6c0.png)
![\sqrt{\frac{a ^{2 } b + a b ^{2 } }{x y } } \cdot \sqrt[6
]{\frac{( a + b ) ^{2 } }{x ^{2 } } } \cdot \sqrt[6 ]{\frac{x ^{2 } y ^{3
} }{( a + b ) ^{2 } } } \cdot \sqrt[4 ]{\frac{x }{a ^{3 } b ^{2 } + a ^{2
} b ^{3 } } }](_images/math/9d4c79d6a2548b452272a623cc787755d468723a.png) R.
R.
![\sqrt[4 ]{\frac{a + b }{x } }](_images/math/61f046d4c8256c72ffec5d5e94d8048f0c349826.png)
![\frac{\sqrt{\frac{x }{y } + \frac{y }{x } } \div \sqrt[3 ]{\frac{x
}{y } - \frac{1 }{x } } }{\sqrt{\frac{xy }{x + y } } }](_images/math/93dba6febcdb0a7b02c780da21d0cdd26c4972c7.png)
Portare uno o più fattori fuori dal segno di radice¶
Trasporta dentro la radice i fattori esterni, discutendo i casi letterali
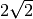 R.
R.
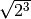 ,
,
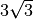 ,
,
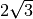 ,
,
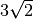 ,
,
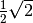 ,
,
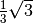
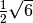 R.
R.
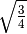 ,
,
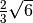 ,
,
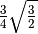 ,
,
![2 \sqrt[3 ]{2 }](_images/math/3436d5c2e14ac675b13cf077caf0f6be01201cf1.png) ,
,
![\frac{1 }{3 } \sqrt[3 ]{3 }](_images/math/b6c20867042c2970664c132cc7a12e344dce54ef.png) ,
,
![4 \sqrt[3 ]{\frac{1 }{2 } }](_images/math/b7544f770380a89407b3b231022d79b0e6c5e8e5.png)
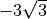 ,
,
![- 2 \sqrt[3 ]{2 }](_images/math/5179b01b87d19563d38611b4246da0c128bc992f.png) ,
,
![\frac{- 1 }{2 } \sqrt[3 ]{4 }](_images/math/7a7cf149b02bfb14f044682728f8c314a4f2287c.png) ,
,
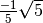 R.
R.
![- \sqrt[3 ]{\frac{1 }{2 } }](_images/math/42cf92ba6cb972c6e92feb80d58687cbe99a3273.png) ,
,
![- \frac{1 }{3 } \sqrt[3 ]{9 }](_images/math/c470e9ec7a757e7142fc50266beb23095c2eced1.png) ,
,
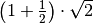
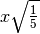 ,
,
![x ^{2 } \sqrt[3 ]{x }](_images/math/3df56bfbcf51dac1bf723180847534db48b5b257.png) R.
R.
![\sqrt[3 ]{x ^{7 } }](_images/math/a01f0d5ffa8bf84e1966f166723dbe601f36d19e.png) ,
,
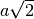 ,
,
![x ^{2 } \sqrt[3 ]{3 }](_images/math/48610609d31c0a263a13c69881f1252768816b6c.png) ,
,
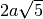 ,
,
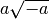
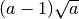 R.
R.
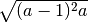 ,
,
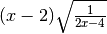 ,
,
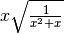
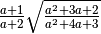 ,
,
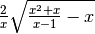 ,
,
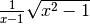
Semplifica i radicali portando fuori tutti i fattori possibili, facendo attenzione al valore assoluto
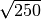 R.
R.
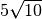 ,
,
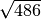 R.
R.
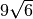
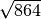 R.
R.
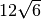 ,
,
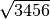 R.
R.
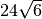
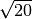 ,
,
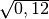 ,
,
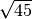 ,
,
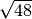
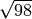 ,
,
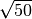 ,
,
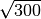 R.
R.
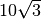 ,
,
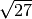
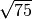 ,
,
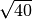 ,
,
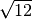 ,
,
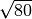
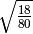 ,
,
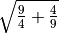 R.
R.
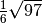 ,
,
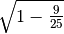 ,
,
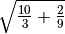
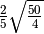 ,
,
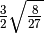 ,
,
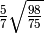 R.
R.
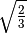 ,
,
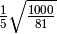
![\sqrt[3 ]{250 }](_images/math/a952270a66ec2d4e64c91d977cf2373ce87a7634.png) ,
,
![\sqrt[3 ]{24 }](_images/math/029519a9face7882c9f7fa64d3f0d2ce91d86e0f.png) ,
,
![\sqrt[3 ]{108 }](_images/math/98d12a84c05d2d1bf9f9ec536962db089eace6f3.png) ,
,
![\sqrt[4 ]{32 }](_images/math/375c7850470a8d8e6bd9c45b18421cad63f2ffe4.png)
![\sqrt[4 ]{48 }](_images/math/e328c86dbf7b694b7f6d451fb258233b18922cb9.png) ,
,
![\sqrt[4 ]{250 }](_images/math/2f4e7a047a4694a2f2276f3bd9ee81367ba9e8b4.png) ,
,
![\sqrt[5 ]{96 }](_images/math/623f1c7e89438370dd6c259fc48a3340ddd71524.png) ,
,
![\sqrt[5 ]{160 }](_images/math/29b47db33beda7eea281573907af19f47a5530ab.png)
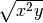 ,
,
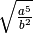 ,
,
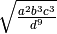 ,
,
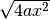
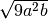 R.
R.
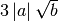 C.E.b>=0,
C.E.b>=0,
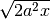 ,
,
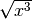 ,
,
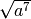
![\sqrt[3 ]{16 a ^{3 } x ^{4 } }](_images/math/51b18be7060233450c5ea6a7dc115fa8fb4b775b.png) ,
,
![\sqrt[3 ]{4 a ^{4 } b ^{5 } }](_images/math/040349f885f8430496d763c98ee3d00499da4725.png) ,
,
![\sqrt[3 ]{27 a ^{7 } b ^{8 } }](_images/math/3e83afe68ff61b439bea901656d1f1a49aa7b056.png) ,
,
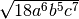
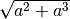 ,
,
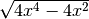 R.
R.
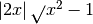 C.E.
C.E.
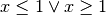 ,
,
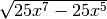 ,
,
![\sqrt[3 ]{3 a ^{5 } b ^{2 } c ^{9 } }](_images/math/b32dc67cc4f728a3152a324d565b58c9108c6e9b.png)
![\sqrt[4 ]{16 a ^{4 } b ^{5 } c ^{7 } x ^{6 } }](_images/math/84f6d4772abb4a3f580da856e6fd2f863e5759b3.png) ,
,
![\sqrt[5 ]{64 a ^{4 } b ^{5 } c ^{6 } d ^{7 } }](_images/math/76a78bff2706b7fd670fa063b06677d12c6b1f21.png) ,
,
![\sqrt[6 ]{a ^{42 } b ^{57 } }](_images/math/ae547751934802811b0fe55e0c7f5c53d8a769e6.png) ,
,
![\sqrt[7 ]{a ^{71 } b ^{82 } }](_images/math/c314ef30897a58000005a22cb067e7666f165ca7.png)
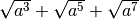 R.
R.
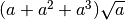
Potenza di radice e radice di radice¶
Esegui le seguenti potenze di radici
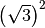 ,
,
![\left( \sqrt[3 ]{2 } \right) ^{3 }](_images/math/e6181a09774ff2c62941c5ee5822cc5722dc221a.png) ,
,
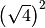 ,
,
![\left( \sqrt[4 ]{2 } \right) ^{6 }](_images/math/76ce11978089f15c5d2f3ba6047dc1b8988216d5.png) R.
R.
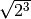
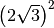 ,
,
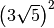 ,
,
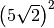 R. 50,
R. 50,
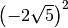
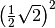 ,
,
![\left( \frac{2 }{3 } \sqrt[4 ]{\frac{2 }{3 } } \right) ^{2 }](_images/math/825fa8c6ca0ffb32b6a1f643b931c3f86ebef6bb.png) ,
,
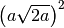 R.
R.
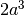 ,
,
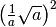
![\left( 2 \sqrt[3 ]{3 } \right) ^{3 }](_images/math/eb72f1fd7b6279a5fbf1399f9ff29551453415b5.png) ,
,
![\left( 3 \sqrt[3 ]{3 } \right) ^{3 }](_images/math/6f85c6280e5fabf46fc6b88eb6ed9b44bdb18b23.png) ,
,
![\left( \frac{1 }{3 } \sqrt[3 ]{3 } \right) ^{3 }](_images/math/a64f66a7d75b15fab854a7694502a2a027bab3a2.png) R
R
 ,
,
![\left( \frac{1 }{9 } \sqrt[3 ]{9 } \right) ^{3 }](_images/math/7d971ebea1160968415afe5e2323a484bdbb1745.png)
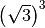 ,
,
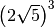 ,
,
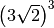 ,
,
![\left( \sqrt[3 ]{2 } \right) ^{6 }](_images/math/1d2b8b1bfb3ec22733e2b0d8b1f38cc45de4c211.png)
![\left( \sqrt[3 ]{3 } \right) ^{6 }](_images/math/e18608220b0bbd235fa05c9622f63c4580e3dfa4.png) ,
,
![\left( \sqrt[3 ]{5 } \right) ^{5 }](_images/math/f0f6c3451c717ab9e2123e71621947ae26e7e12d.png) ,
,
![\left( \sqrt[3 ]{2 } \right) ^{6 }](_images/math/1d2b8b1bfb3ec22733e2b0d8b1f38cc45de4c211.png) ,
,
![\left( \sqrt[6 ]{3 } \right) ^{4 }](_images/math/318be92efaf6d4bb13c55f478845baff442abbba.png)
![\left( \sqrt[6 ]{3 a b ^{2 } } \right) ^{4 }](_images/math/d59d7a5a7a70e2bd4d9257f4b87eced49df52dc2.png) ,
,
![\left( \sqrt[4 ]{16 a ^{2 } b ^{3 } } \right) ^{2 }](_images/math/ef6a748a56eb1628f385e1612032427430557281.png) R.
R.
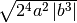 ,
,
![\left( \sqrt[3 ]{6 a ^{3 } b ^{2 } } \right) ^{4 }](_images/math/f27c8a1f6c858b5ce955b037e049a7e06a4bfa1d.png) ,
,
![\left( \sqrt[3 ]{81 a b ^{4 } } \right) ^{4 }](_images/math/351468fd90cfb081bc4dc295ab96c32d4e4a6cfe.png)
Esegui le seguenti radici di radici
![\sqrt[3 ]{\sqrt{2 } }](_images/math/afba2bc48220f6a464b91b8a63cc35a5f3f683ac.png) ,
,
![\sqrt[3 ]{\sqrt[3 ]{16 } }](_images/math/1e306c4d7e9a809ab94bc8a2758309a4bb7dcb4b.png) ,
,
![\sqrt[3 ]{\sqrt[4 ]{15 } }](_images/math/80d04563fad5fae76bc032d84317c7d88e520d6a.png) ,
,
![\sqrt[5 ]{\sqrt{a ^{5 } } }](_images/math/038c8f3b82cad33195e86f3d7d324dca459f8be9.png)
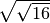 ,
,
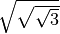 ,
,
![\sqrt[5 ]{\sqrt{a ^{10 } } }](_images/math/db101b7938814088e9534e10cae8932f6002d84c.png) ,
,
![\sqrt[3 ]{\sqrt{\sqrt[3 ]{a ^{12 } } } }](_images/math/58ddd4808e1c7750ef1bcd61f9aa6650075b8fa5.png) R.
R.
![\sqrt[3 ]{a ^{2 } }](_images/math/4f6548a7ce202aef9560862d215f12706448702d.png)
![\sqrt{\sqrt[3 ]{3 a } }](_images/math/e09fcfefaf75bc2c05d0b3cefef68b195dc1d771.png) ,
,
![\sqrt{\sqrt[4 ]{3 a b } }](_images/math/654f56aa2dfd4f9e8ad5b2e1ffb7acd6d8302549.png) ,
,
![\sqrt[3 ]{\sqrt{( a + 1 ) ^{5 } } }](_images/math/7033ee187d53763010f38e53f21b19eb314eb906.png) ,
,
![\sqrt[4 ]{\sqrt{( 2a ) ^{5 } } }](_images/math/017557cb549ffb60261e55c001fb5467f35a015f.png)
![\sqrt{2 ( a - b ) } \cdot \sqrt{\sqrt[3 ]{\frac{1 }{4 a - 4 b } }
}](_images/math/928ff0a378a93ce3d8aad9ad74a2da9d340a3282.png) ,
,
![\sqrt{3 ( a + b ) } \cdot \sqrt{\sqrt[3 ]{\frac{1 }{3 a + 3 b } }
}](_images/math/f8e83a6833ee5880619bd35822d67185990e5479.png) R.
R.
![\sqrt[3 ]{3 ( a + b ) }](_images/math/46a30a8bd6b9608362bac73f2b59eeb767857b26.png) C.E.
C.E.
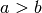 .
.
Somma di radicali¶
Esegui le seguenti operazioni con radicali
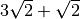 ,
,
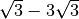
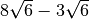 R.
R.
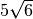 ,
,
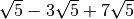
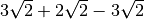 ,
,
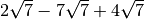 R.
R.
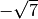
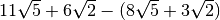 R.
R.
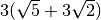
![5 \sqrt{3 } + 3 \sqrt{7 } - [ 2 \sqrt{3 } - ( 4 \sqrt{7 } - 3 \sqrt{3
} ) ]](_images/math/5c051d5b7f28e5c9c9c53400c8e3c7a31c238778.png) R.
R.
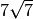
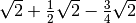 ,
,
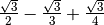
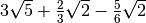 R.
R.
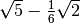
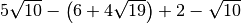 ,
,
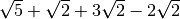
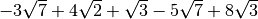 ,
,
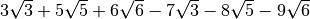
![\sqrt[3 ]{2 } + 3 \sqrt[3 ]{2 } - 2 \sqrt{2 } + 3 \sqrt{2
}](_images/math/bf29ac32dd509e7c2ec6c36bc1170638c742e9a8.png) ,
,
![5 \sqrt{6 } + 3 \sqrt[4 ]{6 } - 2 \sqrt[4 ]{6 } + 3
\sqrt[3 ]{6 } - 2 \sqrt{6 }](_images/math/2e3091a70bed0efe06ab7b4c1170f57771a357a4.png)
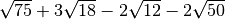 R.
R.
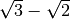
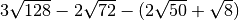 R. 0
R. 0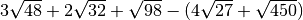 R. 0
R. 0![\sqrt[4 ]{162 } - \sqrt[4 ]{32 } + 5 \sqrt[3 ]{16 } - \sqrt[3 ]{54 } +
\sqrt[3 ]{250 }](_images/math/4b9ce6679ed8c1b35d67890ff20d89840250c547.png) R.
R.
![\sqrt[4 ]{2 } + 12 \sqrt[3 ]{2 }](_images/math/5389bd57d9781aa70480ed3b40e1169f2da1e0ca.png)
![2 \sqrt[3 ]{54 } - \sqrt[4 ]{243 } + 3 \sqrt[4 ]{48 } - \sqrt[3 ]{250
}](_images/math/c4e69786de2d210ee7521a99a75ef488571e6630.png) R.
R.
![\sqrt[3 ]{2 } + 3 \sqrt[4 ]{3 }](_images/math/b260a0884e541039ce2586547fbb03da0b1478c5.png)
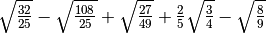 R.
R.
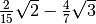
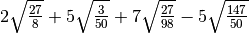 R. 0
R. 0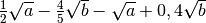 R.
R.
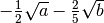
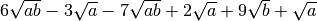 R.
R.
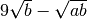
![\sqrt[3 ]{a - b } + \sqrt[3 ]{a ^{4 } - a ^{3 } b } - \sqrt[3 ]{ab ^{3
} - b ^{4 } }](_images/math/4e6014b037a11b789a755215b3c0a97832b6571e.png) R.
R.
![( 1 + a - b ) \sqrt[3 ]{a - b }](_images/math/92908570f8a144ce1199dae629fbe9c4fce5b68c.png)
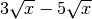
![2 \sqrt[3 ]{x ^{2 } } + 3 \sqrt{x } + 3 \sqrt[3 ]{x ^{2 } }
- 2 \sqrt{x }](_images/math/2c4465abfd6e4b22ae3db0941fbe5e1df6cd5afb.png)
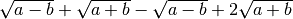 ,
,
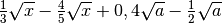
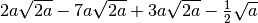 ,
,
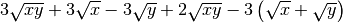
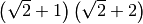 ,
,
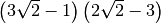
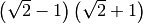 ,
,
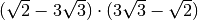
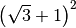 R.
R.
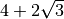 ,
,
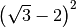 R.
R.
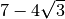
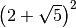 R.
R.
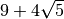 ,
,
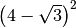 R.
R.
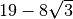
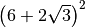 R.
R.
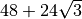 ,
,
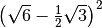 R.
R.
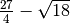
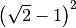 ,
,
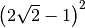
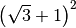 ,
,
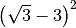
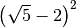 ,
,
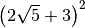
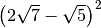 ,
,
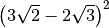
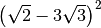 ,
,
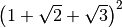
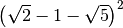 R.
R.
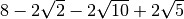
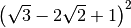 .
.
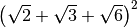
![\left( \sqrt[3 ]{2 } - 1 \right) ^{3 }](_images/math/3f36af7556b04fe5b36b9e5d73cc0d9487f7fdcc.png) R.
R.
![1 - 3 \sqrt[3 ]{4 } + 3 \sqrt[3 ]{2 }](_images/math/de5a05e4db1d6b7a0b474da6795b1538097674b7.png)
![\left( \sqrt[3 ]{3 } + 1 \right) ^{3 }](_images/math/5f9d2dacc1de3bddeba2928e52201f8e548fbd5c.png) ,
,
![\left( \sqrt[3 ]{2 } - 2 \right) ^{3 }](_images/math/0e20f55ce41f549dadbcb8a844c339f7b117d8c5.png)
![\left( \sqrt[3 ]{3 } + \sqrt[3 ]{2 } \right) ^{3 }](_images/math/aa112a3d03135458709c7f86347180d291dc67ba.png) ,
,
![\left( \sqrt[3 ]{3 } + \sqrt[3 ]{2 } \right) \left( \sqrt[3 ]{9 } -
\sqrt[3 ]{4 } \right)](_images/math/4852e41495d87a259594340e2c6ad91f22680767.png)
![\left[ \left( \sqrt[4 ]{2 } + 1 \right) \left( \sqrt[4 ]{2 } - 1
\right) \right] ^{2 }](_images/math/26d1fb607ac4fdabf061b0fd68e78527f8b56fef.png) ,
,
![\left( \sqrt[3 ]{2 } + \sqrt[3 ]{3 } \right) \left( \sqrt[3 ]{4 } -
\sqrt[3 ]{6 } + \sqrt[3 ]{9 } \right)](_images/math/94ec60a5c26752527450f4113d00b2fd4e8bee49.png)
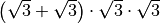 ,
,
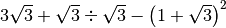
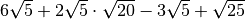 R.
R.
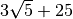 ,
,
![\left( \sqrt[3 ]{a } - \sqrt[3 ]{2 } \right) \left( \sqrt[3 ]{a
^{2 } } + \sqrt[3 ]{2 a } + \sqrt[3 ]{4 } \right)](_images/math/790c664d05353f6e282d8e2cf651f4359c9a6e20.png)
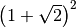 ,
,
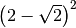
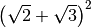 ,
,
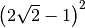
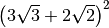 ,
,
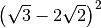
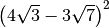 ,
,
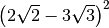 R.
R.
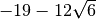
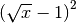 ,
,
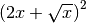
![\left( x + \sqrt[3 ]{x } \right) ^{3 }](_images/math/e644c5e2efd2f88955cd0a7a2080b9f9c0c15fc7.png) ,
,
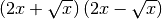
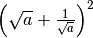 R.
R.
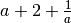 ,
,
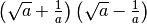
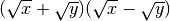 R.
R.

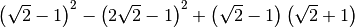
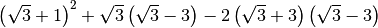
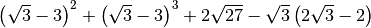
![\left( \sqrt{5 } - 2 \right) ^{2 } - \left( 2 \sqrt{5 } + 3 \right)
^{2 } + \left[ \left( \sqrt{5 } - \sqrt{2 } \right) ^{2 } + 1 \right]
\left( \sqrt{5 } + \sqrt{2 } \right)](_images/math/a2556d8983ad281680da95f1c0eee0292f7b5010.png)
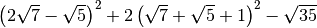
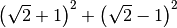 R. 6
R. 6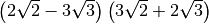
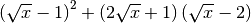
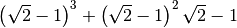
![2 \sqrt{54 } - \sqrt[4 ]{243 } + 3 \sqrt[4 ]{48 } -
\sqrt[3 ]{250 }](_images/math/1a4fa9781a59f5fe7069588ea0a4ee94b9da19fe.png)
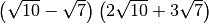
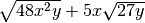
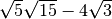
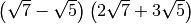
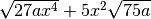
![\sqrt{125 } + 3 \sqrt[6 ]{27 } - \sqrt{45 } - 2 \sqrt[4
]{9 } + \sqrt{20 } + 7 \sqrt[8 ]{81 }](_images/math/eaad573570c02b3e9bd7c6364ddd7d800861ca8d.png)
![\sqrt[3 ]{a \sqrt{a } } \cdot \sqrt{a \sqrt[3 ]{a } } \cdot
\sqrt[3 ]{a \sqrt[3 ]{a } } \cdot \sqrt[3 ]{a \sqrt{a } } \cdot
\sqrt[9 ]{a ^{8 } }](_images/math/f3f2c472e6e18445cf8752bf336991248f557c86.png)
![\sqrt[5 ]{b \sqrt[3 ]{b ^{2 } } } \cdot \sqrt{b ^{2 } \sqrt{b
\sqrt{b ^{2 } } } } \div \sqrt[5 ]{b ^{4 } \sqrt[3 ]{b ^{2 } } } \cdot
\sqrt{b }](_images/math/59eca9b95c8976085bb81adf359a9bf64512704d.png) R.
R.
![\sqrt[5 ]{b ^{7 } }](_images/math/671b3c331a898c2abdb2489ae2cd71bff44a4866.png)
![\sqrt[3 ]{\frac{x }{y ^{3 } } - \frac{1 }{y ^{2 } } } + \sqrt[3 ]{x y
^{3 } - y ^{4 } } - \sqrt[3 ]{8 x - 8 y }](_images/math/8e7c555238cf847d565ea91713f3077cae1216ea.png)
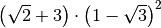
![\left( \sqrt[3 ]{2 } + 3 \right) \cdot \left( 1 - \sqrt[3 ]{3 }
\right) ^{2 }](_images/math/c8201a85f97e09f656b0b3e3cf5b12c990dbf237.png)
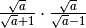
![\sqrt[5 ]{b \sqrt[3 ]{b ^{2 } } } \cdot \sqrt{b \sqrt{b \sqrt{b
^{2 } } } } \div \left( \sqrt[5 ]{b \sqrt[3 ]{b ^{2 } } } \cdot
\sqrt{b } \right)](_images/math/b5a8e03391c6ebddc4bad6391728cef8a8ef0697.png) R.
R.
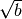
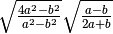
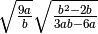
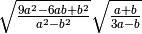
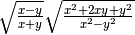
![\sqrt[3 ]{\frac{a }{a + 3 } \sqrt{\frac{a }{a + 3 } \sqrt{\frac{a }{a
+ 3 } } } } \div \sqrt{\frac{a }{a + 3 } }](_images/math/34df88bb4ad0d899c1b8010473e3f73dbe09883d.png) R.
R.
![\sqrt[12 ]{\frac{a }{a + 3 } }](_images/math/1e8099aa886bb0834c33ca6b7dc5c93e99ebe8d7.png)
![\sqrt{\frac{x - 1 }{x + 1 } \sqrt{\frac{x - 1 }{x + 1 } \sqrt{\frac{1
}{x ^{2 } - 31 } } } } \cdot \sqrt[4 ]{x + 1 }](_images/math/b98e61392f15f09a0ffd573c1ecc67f8cfa41f14.png) R.
R.
![\sqrt[8 ]{\left( \frac{x - 1 }{x + 1 } \right) ^{5 } }](_images/math/4376b450fa5b564cb554141a178892b6dac548f5.png)
![\sqrt{\frac{a ^{2 } - 2 a + 1 }{a ( a + 1 ) ^{3 } } } \cdot
\sqrt[4 ]{\frac{a ^{2 } }{( a + 1 ) ^{2 } } } \cdot \sqrt[3 ]{\frac{( a +
1 ) ^{3 } }{( a - 1 ) ^{2 } } }](_images/math/760b42bd79854c3e9370215ca520a317c8ebe895.png) R.
R.
![\sqrt[3 ]{\frac{a - 1 }{( a + 1 ) ^{3 } } }](_images/math/3dd4634ea04aec4cef44a55141befb87069839fc.png)
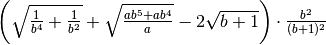 R.
R.
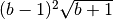
![\left( \sqrt[3x ]{y ^{x } \sqrt[4x ]{y } } + \sqrt[6 ]{y ^{2 }
\sqrt[2x ^{2 } ]{y } } \right) \cdot \sqrt[3 ]{y \sqrt[4x ^{2 }
]{\frac{1 }{y } } }](_images/math/f2eca46761fc00a22c81cfdeb434f7b3517faac5.png) R.
R.
![2 \sqrt[3 ]{y ^{2 } }](_images/math/c5f3574a0a0b1ae5bcb9c07a69925fed1c526666.png)
![\sqrt[4 ]{\frac{b ^{2 } - 1 }{b } } \cdot \sqrt[3 ]{\frac{3b - 3
}{6 b ^{2 } } } \div \sqrt[6 ]{\frac{( b - 1 ) ^{4 } }{4 b ^{5 } } }](_images/math/e6812e99e07a0272731216760e22cfbfa30fc54a.png) R.
R.
![\sqrt[12 ]{\frac{( b + 1 ) ^{3 } }{b ( b - 1 ) } }](_images/math/8450dfeaa3e6e737b800e0416aad5e185c699624.png)
![\sqrt[3 ]{\frac{a ^{2 } + 2 a + 1 }{ab - b } } \cdot \sqrt[6
]{\frac{a ^{2 } - 2 a + 1 }{ab + b } } \cdot \sqrt[4 ]{\frac{b ^{2 } ( a
- 1 ) ^{2 } }{2 a ^{2 } + 4 a + 2 } }](_images/math/89e7a732bfa9e0833ad5e8dce26cd4cda6e90d42.png) R.
R.
![\sqrt[4 ]{\frac{( a - 1 ) ^{2 } }{2 } }](_images/math/6ea95250365785ea845e4afa50d7cc451d489225.png)
![\sqrt[3 ]{\frac{x ^{2 } + 2 xy + y ^{2 } }{x + 3 } } \cdot \sqrt[3
]{\frac{5 x }{x ^{2 } + 6 x + 9 } } \cdot \sqrt[3 ]{\frac{x + y }{5 x }
}](_images/math/2920fa0276df57c160c0102bb6924c7ca949cf66.png) R.
R.
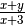
![\sqrt[3 ]{\frac{x ^{2 } - x }{x + 1 } } \cdot \sqrt[15 ]{\frac{x
^{2 } + 2 x + 1 }{x ^{2 } - 2 x + 1 } } \div \sqrt[5 ]{\frac{x - 1 }{x +
1 } }](_images/math/62ea270aebe5b3d4e9a948c610737329a04434c2.png) R.
R.
![\sqrt[3 ]{x }](_images/math/0c7d1ddf7e6b1eea0466e95746ccdf5830ede90c.png)
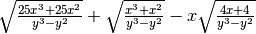
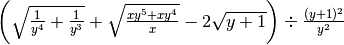 R.
R.
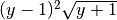
![\sqrt[4 ]{\frac{a ^{2 } - a }{( a + 1 ) ^{2 } } } \cdot \sqrt[12
]{\frac{a ^{2 } - 2 a + 1 }{( a - 1 ) ^{7 } } } \div \sqrt[3 ]{\frac{2 a
^{2 } - 2 a + 1 }{a ^{3 } - a ^{2 } } - \frac{1 }{a - 1 } }](_images/math/8598c62582d43be460aa5dcf11c1a00a5c9e839a.png) R.
R.
![\sqrt[12 ]{\frac{a ^{11 } }{( a ^{2 } - 1 ) ^{6 } } }](_images/math/1d393251b777414a9250e7fbafe34cc1a53acd4b.png)
![\sqrt{\frac{a ^{2 } b + a b ^{2 } }{x y } } \cdot \sqrt[6
]{\frac{( a + b ) ^{2 } }{x ^{2 } } } \cdot \sqrt[6 ]{\frac{x ^{2 } y ^{3
} }{( a + b ) ^{2 } } \cdot \sqrt[4 ]{\frac{x }{a ^{3 } b ^{2 } + a ^{2 } b
^{3 } } } }](_images/math/df3b4021191e7339ec02da10019ad7f00a4b21bc.png) R.
R.
![\sqrt[24 ]{\frac{a ^{10 } b ^{10 } ( a + b ) ^{11 } }{x ^{11 } } }](_images/math/6afb0b9f2b34a8ae26320fedd383da009dadbed5.png)
![\sqrt[6 ]{\frac{1 }{x } + 4 x - 4 } \cdot \sqrt[3 ]{\frac{1 }{x }
+ 4 x + 4 } \cdot \sqrt{\frac{x }{4 x ^{2 } - 1 } }](_images/math/e632bdf023a025e49716b9445d013bb72e5f2b45.png) R.
R.
![\sqrt[6 ]{\frac{2 x + 1 }{2 x - 1 } }](_images/math/326de7cabd5cd19133be2fb1bb2dcdc32962c0c5.png)
![\sqrt{\frac{a ^{2 } - 2 a + 1 }{a ( a + 1 ) ^{3 } } } \cdot
\sqrt[4 ]{\frac{a ^{2 } }{( a + 1 ) ^{2 } } } \cdot \sqrt[3 ]{\frac{( a +
1 ) ^{2 } }{( a - 1 ) ^{2 } } }](_images/math/40ffcffc92a28a676cf0f8845fc8bb3b68c9a4af.png) R.
R.
![\sqrt[3 ]{\frac{a - 1 }{( a + 1 ) ^{2 } } }](_images/math/344644f8ddc5972ea7f2c8bd943bd41a4f3e77e4.png)
![\left( \sqrt[3 ]{\frac{a }{3 } - 2 + \frac{3 }{a } } \cdot \sqrt[6
]{\frac{9 a ^{2 } ( a + 3 ) ^{3 } }{( a - 3 ) ^{2 } } } \right) \div
\sqrt{\frac{a ^{2 } - 9 }{3 a } }](_images/math/d07c4672201a9974ffce506a9839e7c53ce30b19.png) R.
R.
![\sqrt[6 ]{\frac{27 a ^{3 } }{a - 3 } }](_images/math/9de050510460fd796226addb239a04537bf0e14f.png)
![\sqrt[4 ]{\frac{a ^{3 } - a ^{2 } }{( a + 1 ) ^{2 } } } \cdot
\sqrt[12 ]{\frac{a ^{2 } - 2 a + 1 }{( a - 1 ) ^{7 } } } \cdot \sqrt[3
]{\frac{2 a ^{2 } - 2 a + 1 }{a ^{3 } - a ^{2 } } - \frac{1 }{a - 1 } }](_images/math/150d76978d776429fe2e1b81a1ceecb9e9ab859b.png) R.
R.
![\sqrt[6 ]{\frac{a - 1 }{a ( a + 1 ) ^{3 } } }](_images/math/2ccedccf30d19c50913baad9083503e2a21a0441.png)
![\sqrt{1 - \frac{1 }{y } + \frac{1 }{4 y ^{2 } } } \div \left(
\sqrt[6 ]{\frac{1 }{8 y ^{3 } + 12 y ^{2 } + 6 y + 1 } } \cdot \sqrt{1 -
\frac{1 }{4 y ^{2 } } } \right)](_images/math/d4e6513ade37659306afc79ab2bfe5710c95284c.png) R.
R.
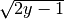
![\sqrt[3 ]{1 - \frac{1 }{a } + \frac{1 }{4 a ^{2 } } } \div \left(
\sqrt{1 - \frac{1 }{4 a ^{2 } } } \cdot \sqrt[6 ]{\frac{1 }{8 a ^{3 } +
12 a ^{2 } + 6 a + 1 } } \right)](_images/math/18965f892884c91f1c7dffd627b6b11eb0cd1872.png) R.
R.
![\sqrt[6 ]{4 a ^{2 } ( 2 a - 1 ) }](_images/math/6c248cdb049a39e038466efb7799b492a47b43b5.png)
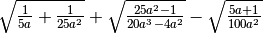 R.
R.
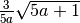
![\sqrt[3 ]{\frac{x }{y ^{3 } } - \frac{1 }{y ^{2 } } } + \sqrt[3 ]{x y
^{3 } - y ^{4 } } - \sqrt[3 ]{8x - 8y }](_images/math/7340b24384cfcc287ae4e7018186b5dabd757e23.png) R.
R.
![\frac{( 1 - y ) ^{2 } }{y } \sqrt[3 ]{x - y }](_images/math/a42feb4654c5feb71f75c81d5193b378ef91781c.png)
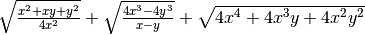 R.
R.
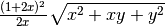
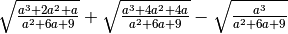 R.
R.
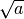
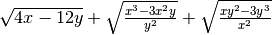 R.
R.
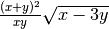
![\left( \sqrt[6 ]{\frac{1 }{x ^{2 } - 2 x + 1 } } + \sqrt[6 ]{\frac{64
a ^{6 } }{x ^{2 } - 2 x + 1 } } + \sqrt[6 ]{\frac{a ^{12 } }{x ^{2 } - 2 x +
1 } } \right) \cdot \sqrt[3 ]{x - 1 }](_images/math/f8f475fe330f1321eb5f008d985fc5d0a82cd1d5.png) R.
R.
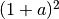
![\left( \sqrt[3x ]{y ^{x } \sqrt[4x ]{y } } + \sqrt[6 ]{y ^{2 }
\sqrt[2x ^{2 } ]{y } } \right) \cdot \sqrt[4x ^{2 } ]{\frac{1 }{y } }](_images/math/05ba658e7f11aee89859871e5f0e590d7fc9f1fc.png)
Esegui le seguenti operazioni trasformando i radicali in potenze con esponente frazionario.
![\sqrt{a \sqrt[3 ]{a \sqrt[3 ]{a ^{2 } } } } \cdot \sqrt[3 ]{a
\sqrt[3 ]{\frac{1 }{a } } } \div \sqrt{\frac{1 }{a } }](_images/math/c0e680f797c6cd830f8837bc3b909bdbd8a8709b.png) R.
R.
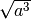
![\sqrt[5 ]{a \sqrt{a ^{3 } } } \cdot \sqrt{a \sqrt[7 ]{\frac{1 }{a
^{2 } } } } \div \sqrt[7 ]{a ^{4 } \sqrt{a } }](_images/math/eee2d75aa3922c8e74b60db7d0b96adda0bacdc0.png) R.
R.
![\sqrt[14 ]{a ^{3 } }](_images/math/9c807ed2c6f5868b9a9fdb5ad911f6e98528fb6d.png)
![\sqrt[3 ]{a \sqrt{a } } \cdot \sqrt[3 ]{a \sqrt[3 ]{a } } \cdot
\sqrt{a \sqrt[3 ]{a } } \cdot \sqrt[3 ]{a \sqrt{a } }](_images/math/7c7244ce7cd042b4d2b431904e2df425b7ed01e6.png) R.
R.
![\sqrt[9 ]{a ^{19 } }](_images/math/cb97cb36d0bdda2787dfb9bd0cb63e7c22d8a475.png)
![\sqrt[5 ]{b \sqrt[3 ]{b ^{2 } } } \cdot \sqrt{b ^{2 } \sqrt{b
\sqrt{b ^{2 } } } } \div \sqrt[5 ]{b ^{4 } \sqrt[3 ]{b ^{2 } } } \cdot
\sqrt{b }](_images/math/59eca9b95c8976085bb81adf359a9bf64512704d.png) R.
R.
![\sqrt[5 ]{b ^{7 } }](_images/math/671b3c331a898c2abdb2489ae2cd71bff44a4866.png)
Razionalizzazione del denominatore di una frazione¶
Razionalizza i seguenti radicali
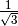 ,
,
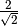 ,
,
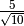 ,
,
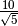 R.
R.
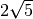
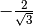 ,
,
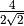 ,
,
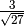 .
.
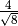 R.
R.
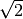
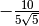 ,
,
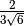 R.
R.
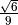 ,
,
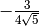 ,
,
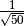
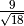 ,
,
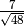 ,
,
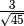 ,
,
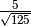
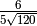 ,
,
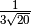 ,
,
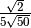 ,
,
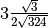
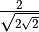 ,
,
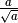 ,
,
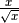 ,
,
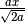
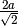 ,
,
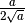 ,
,
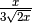 R.
R.
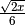 ,
,
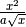
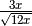 ,
,
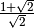 ,
,
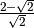 ,
,
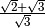
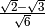 ,
,
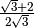 ,
,
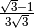 ,
,
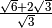
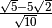 ,
,
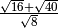 ,
,
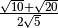 R.
R.
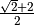 ,
,
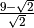
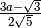 ,
,
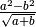 ,
,
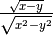 ,
,
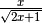
![\frac{1 }{\sqrt[3 ]{2 } }](_images/math/5ac1ff978587eaa4ce3f6c0338ebf00f77ffa8e7.png) ,
,
![\frac{2 }{\sqrt[3 ]{4 } }](_images/math/d2308c2edf2960b98fceaa22aad99b962f1e2103.png) ,
,
![\frac{3 }{\sqrt[3 ]{5 } }](_images/math/3bea36ea10ece7bf45615288570868bd89636f70.png) ,
,
![\frac{4 }{\sqrt[3 ]{6 } }](_images/math/bfe609e46c5a49a5f567021fe92bde4fde1a9df9.png) R.
R.
![\frac{2 }{3 } \sqrt[3 ]{36 }](_images/math/2eb98d536c2e4367818f9eb074c244e89d21c22e.png)
![\frac{1 }{\sqrt[3 ]{2 } }](_images/math/5ac1ff978587eaa4ce3f6c0338ebf00f77ffa8e7.png) ,
,
![\frac{2 }{\sqrt[3 ]{4 } }](_images/math/d2308c2edf2960b98fceaa22aad99b962f1e2103.png) ,
,
![\frac{3 }{\sqrt[3 ]{5 } }](_images/math/3bea36ea10ece7bf45615288570868bd89636f70.png) ,
,
![\frac{4 }{\sqrt[3 ]{6 } }](_images/math/bfe609e46c5a49a5f567021fe92bde4fde1a9df9.png)
![\frac{2 }{3 \sqrt[3 ]{2 } }](_images/math/e655546e414e585202bea137d06a9dd81d07d471.png) ,
,
![\frac{6 }{5 \sqrt[3 ]{100 } }](_images/math/368f21fa21d96c8face7b4ea388e789bfdf1fb2e.png) ,
,
![\frac{2 }{\sqrt[5 ]{9 } }](_images/math/91d42ab2489965ee1a9d43ce1d765052e9a87d23.png) ,
,
![\frac{3 }{2 \sqrt[6 ]{27 } }](_images/math/0c795b7436e64bcc72a0d87870bce79db3526fdd.png)
![\frac{10 }{\sqrt[5 ]{125 } }](_images/math/9bebad52f6536915ef15bc987eb61d77b848a16b.png) ,
,
![\frac{16 }{\sqrt[3 ]{36 } }](_images/math/6b85c69ab10c87812646fd6bab87bf2a79c2f782.png) ,
,
![\frac{9 }{\sqrt[4 ]{2025 } }](_images/math/c8f3c45570490d1934def69ea1e98a9e4559bfea.png) ,
,
![\frac{1 }{\sqrt[5 ]{144 } }](_images/math/15893d52f5175fb32d2e8f0ca7cd21e53783603e.png)
![\frac{a b }{\sqrt[3 ]{a ^{2 } b } }](_images/math/11a77fcee36ba6555c73857be6cfee0d9024c507.png) ,
,
![\frac{a b ^{2 } }{\sqrt[3 ]{a b ^{2 } } }](_images/math/8ab9b70d09b83cfae522839506ee0b590a0f3651.png) R.
R.
![\sqrt[3 ]{a ^{2 } b }](_images/math/8bf22b8c47c2e1e1771e629531f73ba830e2f1ee.png) ,
,
![\frac{3 a ^{2 } b }{\sqrt[4 ]{9 a b ^{3 } } }](_images/math/95f41441c78f9d519e478854096a0aa03ccd5def.png) ,
,
![\frac{2 \sqrt{a } }{\sqrt[4 ]{27 a b ^{2 } c ^{5 } } }](_images/math/66861efec260521abd4461e8b9d45c193e111f11.png)
![\frac{5x }{\sqrt[3 ]{x \sqrt{5 } } }](_images/math/e6d54956f4fe698f6e77be113669e6b6829a804e.png) ,
,
![\frac{2 \sqrt{2 } }{\sqrt[5 ]{16 a ^{2 } b ^{3 } c ^{4 } } }](_images/math/f90e07aa0c226ed33c7d9e489cedf2420a031b63.png) ,
,
![\frac{\sqrt[3 ]{x ^{2 } y } + \sqrt[3 ]{x y ^{2 } } }{\sqrt[3 ]{x y }
}](_images/math/e4fe8b148fcd7dcbc1e930f27ec94b12449ab444.png) ,
,
![\frac{3 - a \sqrt[3 ]{9 } }{\sqrt[3 ]{9 a } }](_images/math/5de0d106e9a38ea6095b97a11d87c405b24d0865.png)
![\frac{1 - \sqrt[3 ]{a } }{\sqrt[3 ]{4 a ^{2 } x } }](_images/math/a45fa666456efe836ee8b1bb64b5c241a0859e98.png) ,
,
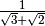 ,
,
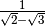 ,
,
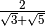
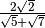 ,
,
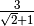 ,
,
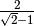 ,
,
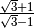
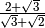 R
R
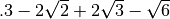 ,
,
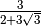 ,
,
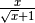 ,
,
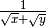
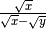 ,
,
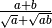 ,
,
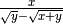 ,
,
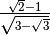
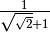 ,
,
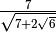 ,
,
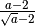 ,
,
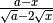
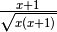 ,
,
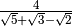 ,
,
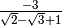 ,
,
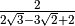
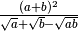 ,
,
![\frac{3 }{\sqrt[3 ]{2 } + \sqrt[3 ]{9 } }](_images/math/9fd78dde459e44774f880d6605c219a39fbdaa80.png) ,
,
![\frac{6 }{\sqrt[3 ]{3 } - \sqrt[3 ]{5 } }](_images/math/00816f2a17d1e4d7c1ea2742e302cf64baa8a0af.png) ,
,
![\frac{\sqrt{6 } }{\sqrt[3 ]{4 } + \sqrt[3 ]{9 } }](_images/math/bd61036c222c23c6c29830f80b12099f95c5744c.png)
![\frac{\sqrt{2 } }{2 \sqrt[3 ]{2 } - 3 \sqrt[3 ]{3 } }](_images/math/dc36cd83b49b9660bae45c5cd4f69870d2e5140d.png) ,
,
![\frac{\sqrt{2 } + 1 }{\sqrt[3 ]{2 } - 1 }](_images/math/9c2d4978b3d4166bcc18f675e848986707c3f6eb.png) ,
,
![\frac{3 }{\sqrt[3 ]{4 } - \sqrt[3 ]{2 } }](_images/math/0fcc8338b3ccc110820caa1c9eb28fce201bc57b.png) ,
,
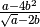
![\frac{2 }{\sqrt[3 ]{2 } - 1 }](_images/math/0e62131358f7d0b0da0bb90920a4e2c8d91a2afa.png) ,
,
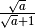 ,
,
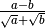 ,
,
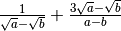
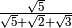 ,
,
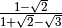 ,
,
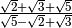 ,
,
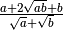
Radicali doppi¶
- Verificate che
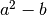 sia un quadrato perfetto prima di applicare la formula di trasformazione
sia un quadrato perfetto prima di applicare la formula di trasformazione 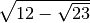 ,
,
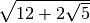 ,
,
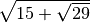 ,
,
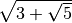 R.
R.
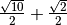
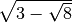 ,
,
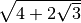 ,
,
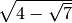 ,
,
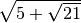
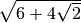 ,
,
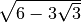 ,
,
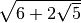 ,
,
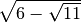
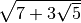 ,
,
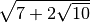 ,
,
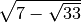 ,
,
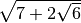 R.
R.
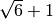
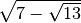 ,
,
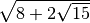 ,
,
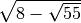 ,
,
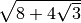
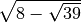 ,
,
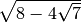 ,
,
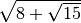 ,
,
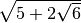
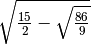 ,
,
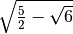 ,
,
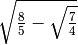 ,
,

Equazioni, disequazioni e sistemi a coefficienti irrazionali¶
Risolvi le seguenti equazioni a coefficienti irrazionali
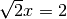 ,
,
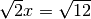 ,
,
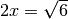 ,
,
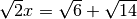
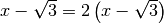 R.
R.
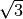 ,
,
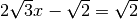 R.
R.
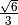
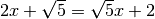 R. 1,
R. 1,
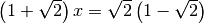 R.
R.
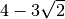
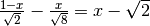 R.
R.
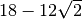 ,
,
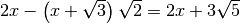 R.
R.
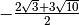
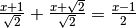 R.
R.
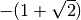
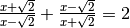 impossibile
impossibile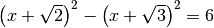 R.
R.
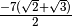
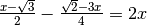 R.
R.
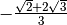
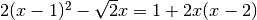 R.
R.
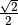
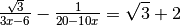 R.
R.
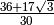
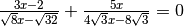 R.
R.
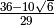
Risolvi le seguenti disequazioni a coefficienti irrazionali
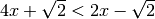 R.
R.
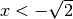
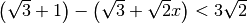 R.
R.
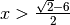
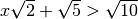 R.
R.
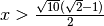
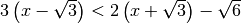 R.
R.
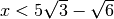
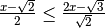 R.
R.
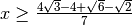
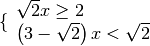 impossibile
impossibile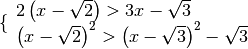 R.
R.
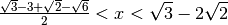
Risolvi i seguenti sistemi a coefficienti irrazionali
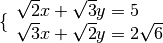 R.
R.
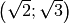 ,
,
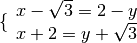 R.
R.
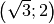
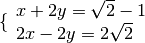 R.
R.
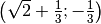 ,
,
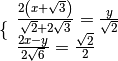 R.
R.
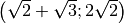
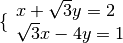 R.
R.
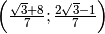 ,
,
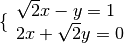 R.
R.
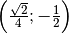
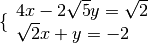 R.
R.
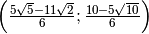
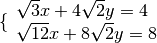 indeterminato
indeterminato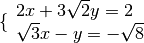 R.
R.
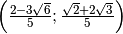
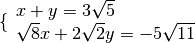 impossibile
impossibile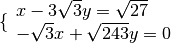 R.
R.
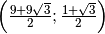
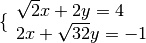 R.
R.
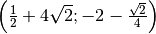
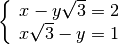 R.
R.
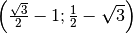
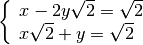 R.
R.
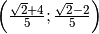
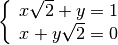 R.
R.
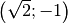
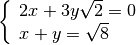 R.
R.
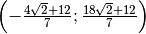
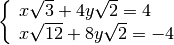 R. impossibile
R. impossibile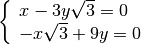 R. indeterminato
R. indeterminato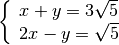 R.
R.
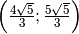
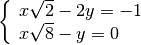 R.
R.
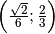
Esercizi di riepilogo¶
Per ciascuna delle seguenti affermazioni indica se è Vera o Falsa.
- È dato un quadrato di lato
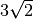 .
.- Il suo perimetro è un numero irrazionale

- La sua area è un numero irrazionale

- Il suo perimetro è un numero irrazionale
- È dato un rettangolo di base
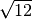 e altezza 14.
e altezza 14.- Il suo perimetro è un numero irrazionale

- La sua area è un numero razionale

- Il perimetro non esiste perché non si sommano numeri razionali con numeri
irrazionali

- La misura del perimetro è un numero sia razionale che irrazionale

- Il suo perimetro è un numero irrazionale
- Un triangolo rettangolo ha i cateti lunghi rispettivamente
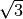 cm e
cm e
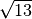 cm.
cm.- L’ipotenusa ha come misura un numero razionale

- Il perimetro è un numero irrazionale

- L’area è un numero irrazionale

- L’ipotenusa ha come misura un numero razionale
- È dato un quadrato di lato
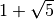
- La misura della diagonale è un numero irrazionale

- L’area è un numero irrazionale

- La misura della diagonale è un numero irrazionale
- È dato un rettangolo di base
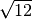 e altezza
e altezza
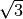 .
.- Il perimetro è un numero irrazionale

- L’area è un numero irrazionale

- La misura della diagonale è un numero irrazionale

- Il quadrato della misura del perimetro è un numero irrazionale

- Il perimetro è un numero irrazionale
- Un triangolo rettangolo ha un cateto lungo 7cm. Determina, se esiste, una possibile misura dell’altro cateto in modo che questa sia un numero irrazionale e che l’ipotenusa sia, invece, un numero razionale.
- Perché l’uguaglianza
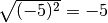 è falsa?
è falsa? - Determina il valore di verità delle seguenti affermazioni
- La radice terza del triplo di
 è uguale ad
è uguale ad
 .
.

- Dati due numeri reali positivi, il quoziente delle loro radici quadrate è
uguale alla radice quadrata del quoziente.

- Il doppio della radice quadrata di a è uguale alla radice quadrata del
quadruplo di a.

- Dati due numeri reali positivi, la somma delle loro radici cubiche è
uguale alla radice cubica della loro somma.

- La radice cubica di 2 è la metà della radice cubica di 8.

- Dati un numero reale positivo, la radice quadrata della sua radice cubica
è uguale alla radice cubica della sua radice quadrata.

- Sommando due radicali letterali simili si ottiene un radicale che ha la
stessa parte letterale dei radicali dati.

- La radice terza del triplo di
- Riscrivi in ordine crescente i radicali
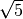 ;
;
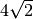 ;
;
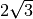
- Verifica che il numero irrazionale
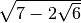 appartiene all’intervallo
appartiene all’intervallo
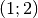 e rappresentalo sull’asse dei numeri reali.
e rappresentalo sull’asse dei numeri reali. - Sono assegnati i numeri
![\alpha = \sqrt[3 ]{( \sqrt{30 } - \sqrt{3 } ) \cdot ( \sqrt{30 } +
\sqrt{3 } ) } + \sqrt[4 ]{( 7 \sqrt{2 } - \sqrt{17 } ) \cdot ( 7 \sqrt{2 } -
\sqrt{17 } ) }](_images/math/a9eefd94de1c2e85a0543af1cf565ca80d12c9d0.png) e
e
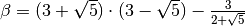 , quali affermazioni sono vere?
, quali affermazioni sono vere?- sono entrambi irrazionali;
- solo
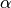 è irrazionale;
è irrazionale; 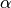 è minore di
è minore di
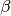 ;
;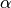 è maggiore di
è maggiore di
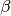 ;
;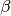 è irrazionale negativo
è irrazionale negativo
- Le misure rispetto al cm dei lati di un rettangolo sono i numeri reali
![l _{1 } = \sqrt[3 ]{1 - \frac{1 }{8 } } \cdot \sqrt[3 ]{1 - \frac{2
}{7 } } \cdot \sqrt[3 ]{25 }](_images/math/316a4364d41f94a24622297d758c63eadfb1b5d5.png) e
e
![l _{2 } = \sqrt{\sqrt{2 } } \cdot \sqrt[4 ]{3 } \cdot ( \sqrt[8 ]{6 }
) ^{3 } \div \sqrt[4 ]{\sqrt{6 } }](_images/math/007ad8bf59fe0ce5723504677a1f9bb6807c2efb.png) . Determinare la misura del perimetro e della diagonale del reattangolo.
. Determinare la misura del perimetro e della diagonale del reattangolo. - Se x è positivo e diverso da 1, l’espressione
![E = \sqrt[4 ]{\frac{4 }{\sqrt{x } - 1 } - \frac{4 }{\sqrt{x } + 1 } }
\div \sqrt[4 ]{\frac{4 }{\sqrt{x } - 1 } + \frac{4 }{\sqrt{x } + 1 } }](_images/math/ce99114cc866319cb83bdfb1d07a4a71ac9edf41.png) è uguale a:
è uguale a: - Stabilire se la seguente affermazione è vera o falsa. Per tutte le coppie
(a,b) di numeri reali positivi con
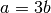 , l’espressione
, l’espressione
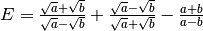 ha il numeratore doppio del denominatore.
ha il numeratore doppio del denominatore. - Calcola il valore delle seguenti espressioni letterali per i valori indicati
delle lettere
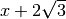 per
per
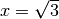
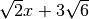 per
per
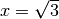
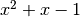 per
per
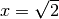
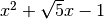 per
per
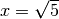
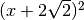 per
per
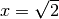
- Trasforma in un radicale di indice 9 il seguente radicale
![\sqrt[3 ]{\frac{\sqrt{\frac{a }{b } - \frac{b }{a } } }{\sqrt{\frac{a
}{b } + \frac{b }{a } + 2 } } \div \sqrt{\frac{a + b }{a - b } } + 1 }](_images/math/9e5d1ee05d6171e9a52684861ef716f023f7cc75.png)
Risolvi le equazioni
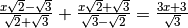
![R. [ - 1 ]](_images/math/aae845d23ad516dfadf8f0e2e558874678ce94bd.png)
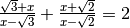
![R. [ 2 \cdot ( 3 \sqrt{2 } - 2 \sqrt{3 } ) ]](_images/math/000b50e122347968ee31ccfc1947e4ab54ed32cc.png)
- Per quale valore di k il sistema lineare è determinato?
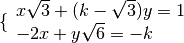
- L’insieme di soluzioni della disequazione
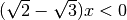 è:
è: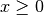
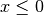
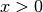

- sempre verificata.
- Stabilire se esistono valori di a che rendono positiva l’espressione:
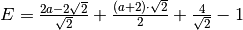
- Data la funzione
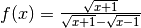
- Determina il suo dominio,
- Riscrivi la funzione razionalizzando il denominatore,
- Calcola f(2),
- Per quali valori di x si ha f(x)>0?
- Risolvi l’equazione f(x)=0izzando il denominatore,
- Calcola f(2),
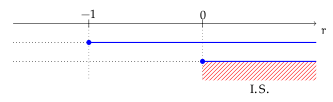
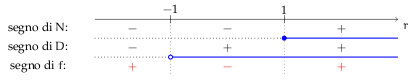
![\sqrt[3 ]{\frac{x ^{2 } }{( x - 1 ) ^{2 } } } \div \sqrt[4 ]{\frac{(
x - 1 ) ^{2 } \cdot ( x + 1 ) ^{2 } }{( x + 1 ) ( x - 1 ) } }](_images/math/081184f0c940982d44f84d82889a91d8e49edc4b.png)

![\sqrt[3 ]{\frac{x ^{2 } }{( x - 1 ) ^{2 } } } \div \sqrt[4 ]{( x - 1
) \cdot ( x + 1 ) }](_images/math/3da1b7ee88fd3d19475cba53f873274d4031a12f.png)
![\sqrt[12 ]{\left[ \frac{x ^{2 } }{( x - 1 ) ^{2 } } \right] ^{4 } }
\div \sqrt[12 ]{( x - 1 ) ^{3 } \cdot ( x + 1 ) ^{3 } }](_images/math/e5a1cfeb9de8db593ce48e0f98391c5af592f9e4.png)
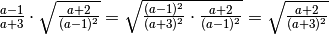
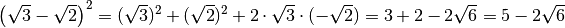
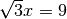
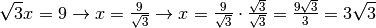
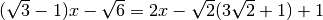
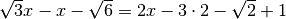 ;tab;
;tab;
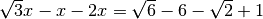
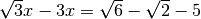
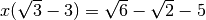
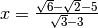
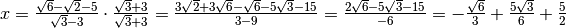
![\sqrt[4 ]{\frac{1 }{x } }](_images/math/3217401c49714795412ad707a4a48c628c88e930.png)
![\sqrt[8 ]{\frac{1 }{x } }](_images/math/c555da8f96435e06bdbf6d77fc5398dc6c3a6746.png)
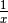
![\sqrt[8 ]{x }](_images/math/379b8632cdc1adb8eba2ca1ab8fc5bfde258f398.png)